题目内容
如图,直线y=-2x+8交x轴于A,交y轴于B i点p在线段AB上,过点P分别向x轴、y轴引垂线,垂足为C、D,设点P的横坐标为m,矩形PCOD的面积为S.
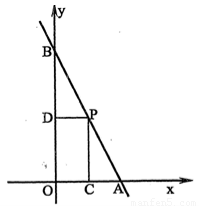
(1)求S与m的函数关系式; (2)当m取何值时矩形PCOD的面积最大,最大值是多少.
【答案】
(1)S与m的函数关系式为S=﹣2m2+8m;
(2)当m=2时,矩形PCOD的面积最大,最大面积为8.
【解析】
试题分析:(1)先求得P的纵坐标,再利用矩形的面积公式即可求得;
(2)根据二次函数的性质,即可确定.
试题解析:(1)由题意可知P(m,﹣2m+8),
∴OC=m,PC=﹣2m+8
S=m(﹣2m+8)=﹣2m2+8m
∴S与m的函数关系式为S=﹣2m2+8m;
(2)∵a=﹣2<0,
∴S有最大值.
当m= 时,
时,
S最大= =8;
=8;
∴当m=2时,矩形PCOD的面积最大,最大面积为8.
考点:一次函数综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 16、如图,直线l1y1:=2x+b与直线l2:y2=-x+3交点为P(1,2),当y1>y2>0时,x的取值范围是
16、如图,直线l1y1:=2x+b与直线l2:y2=-x+3交点为P(1,2),当y1>y2>0时,x的取值范围是
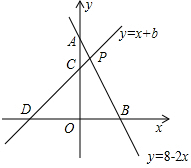 (2004•西藏)已知,如图,直线y=8-2x与y轴交于点A,与x轴交于点B,直线y=x+b与y轴交于点C,与x轴交于点D,如果两直线交于点P,且AC:CO=3:5(AO>CO).
(2004•西藏)已知,如图,直线y=8-2x与y轴交于点A,与x轴交于点B,直线y=x+b与y轴交于点C,与x轴交于点D,如果两直线交于点P,且AC:CO=3:5(AO>CO). 如图,直线与y=2x双曲线
如图,直线与y=2x双曲线
