题目内容
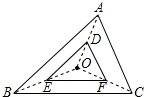如图，△DEF是由△ABC经过位似变换得到的，点O是位似中心，D、E、F分别是OA、OB、OC的中点，则△DEF与△ABC的面积比是（ ）| A、1：2 | B、1：4 | C、1：5 | D、1：6 |
分析：图形的位似就是特殊的相似，满足相似的性质，且位似图形上任意一对对应点到位似中心的距离之比等于相似比．因为D、E、F分别是OA、OB、OC的中点，根据三角形的中位线定理可知：DF=
AC，即△DEF与△ABC的相似比是1：2，所以面积的比是1：4．
| 1 |
| 2 |
解答：解：∵D、F分别是OA、OC的中点，
∴DF=
AC，
∴△DEF与△ABC的相似比是1：2，
∴△DEF与△ABC的面积比是1：4．
故选：B．
∴DF=
| 1 |
| 2 |
∴△DEF与△ABC的相似比是1：2，
∴△DEF与△ABC的面积比是1：4．
故选：B．
点评：本题主要考查了三角形中位线定理，位似的定义及性质：面积的比等于相似比的平方．
练习册系列答案
相关题目
如图，△DEF是由△ABC经过位似变换得到的，点O是位似中心，D，E，F分别是OA，OB，OC的中点，则△DEF与△ABC的面积比是
22、如图，△DEF是由△ABC旋转得到的，请作出它的旋转中心．
如图，△DEF是由直角三角形ABC沿BC方向平移得到的，如果AB=8，BE=4，DH=3，则图中阴影部分的面积为（ ）| A、20 | B、23 | C、26 | D、30 |
如图，△DEF是由△ABC沿AB方向平移2cm得到的，已知△ABC的周长为22cm，则四边形AEFC的周长为