Question

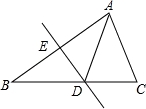
如图，△ABC是等边三角形．P是∠ABC的平分线BD上一点，PE⊥AB于点E，线段BP的垂直平分线交BC于点F，垂足为点Q．若BF=2，则PE的长为__________．

Answer 1

．

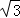【考点】等边三角形的性质；含30度角的直角三角形．

【分析】在直角△BFQ中，利用三角函数即可求得BQ的长，则BP的长即可求得，然后在直角△BPE中，利用30度所对的直角边等于斜边的一半即可求得PE的长．

【解答】解：∵△ABC是等边三角形．P是∠ABC的平分线BD上一点，

∴∠FBQ=∠EBP=30°，

∴在直角△BFQ中，BQ=BF•cos∠FBQ=2×=，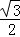

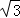又∵QF是BP的垂直平分线，

∴BP=2BQ=2．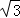

∵直角△BPE中，∠EBP=30°，

∴PE=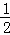BP=．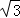

故答案是：．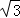

【点评】本题考查了等边三角形的性质以及直角三角形的性质和三角函数，正确求得BQ的长是关键．