Question

【题目】如图，将边长为 的正方形 的一边 与直角边分别是 和 的 的一边 重合．正方形 以每秒 个单位长度的速度沿 向右匀速运动，当点 和点 重合时正方形停止运动．设正方形的运动时间为 秒，正方形 与 重叠部分面积为S，则S关于 的函数图象为（ ）

A. B. C. D.

Answer 1

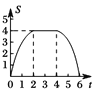
【答案】B

【解析】

分类讨论：当0≤t≤2时，BG=t，BE=2-t，运用△EBP∽△EGF的相似比可表示PB=4-2t，S为梯形PBGF的面积，则S=（4-2t+4）t=-t2+4t，其图象为开口向下的抛物线的一部分；

当2＜t≤4时，S=FGGE=4，其图象为平行于x轴的一条线段；

当4＜t≤6时，GA=t-4，AE=6-t，运用△EAP∽△EGF的相似比可得到PA=2（6-t），所以S为三角形PAE的面积，则S=（t-6）2，其图象为开口向上的抛物线的一部分．

当0≤t≤2时，如图

，

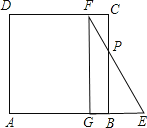BG=t，BE=2-t，

∵PB∥GF，

∴△EBP∽△EGF，

∴，即，

∴PB=4-2t，

∴S=（PB+FG）GB=（4-2t+4）t=-t2+4t；

当2＜t≤4时，S=FGGE=4；

当4＜t≤6时，如图，

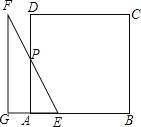
GA=t-4，AE=6-t，

∵PA∥GF，

∴△EAP∽△EGF，

∴，即，

∴PA=2（6-t），

∴S=PAAE=×2×（6-t）（6-t）

=（t-6）2，

综上所述，当0≤t≤2时，s关于t的函数图象为开口向下的抛物线的一部分；当2＜t≤4时，s关于t的函数图象为平行于x轴的一条线段；当4＜t≤6时，s关于t的函数图象为开口向上的抛物线的一部分．

故选：B．