��Ŀ����
 ��2007•��������ģ����֪����PΪ�߶�AB�ϵĶ��㣨��A��B���㲻�غϣ�����ͬһƽ���ڣ����߶�AP��BP�ֱ��۳ɡ�CDP����EFP�����С�CDP=��EFP=90�㣬��D��P��F���㹲�ߣ���ͼ��ʾ��
��2007•��������ģ����֪����PΪ�߶�AB�ϵĶ��㣨��A��B���㲻�غϣ�����ͬһƽ���ڣ����߶�AP��BP�ֱ��۳ɡ�CDP����EFP�����С�CDP=��EFP=90�㣬��D��P��F���㹲�ߣ���ͼ��ʾ����1������CDP����EFP��Ϊ���������Σ���DF=2����AB�ij���
��2����AB=12��tan��C=
| 4 | 3 |
��������1�����ݵ���ֱ�������ε����ʣ���DP=x��PF=y���ó�CD=DP=x��EF=PF=y��PC=
x��PE=
y�������ó�x+y��ֵ�����AB���ɣ�
��2������tan��C=
������C��D��PΪ����������κ���E��F��PΪ��������������ƣ���˷�����������ǣ�����DCP=��PEFʱ������DCP=��EPFʱ���ֱ����ù��ɶ������m+n��ֵ�����ɵó��ı���CDFE���������Сֵ��
| 2 |
| 2 |
��2������tan��C=
| 4 |
| 3 |
����⣺��1����DP=x��PF=y��
�ߡ�CDP�͡�EFP���ǵ���ֱ�������Σ��ҡ�CDP=��EFP=90�㣬
��CD=DP=x��EF=PF=y��PC=
x��PE=
y��
��AB=AP+PB=CD+DP+PC+PF+EF+PE
=x+x+
x+y+y+
y
=��2+
����x+y����
��DF=2��
��x+y=2��
��AB=��2+
����2=4+2
��
��2������CE��
����tan��C=
������C��D��PΪ����������κ���E��F��PΪ��������������ƣ���˷�����������ǣ�
�ٵ���DCP=��PEFʱ��
��DP=4m��PF=4n����CD=3m��EF=3n��
���ݹ��ɶ������ɵ�CP=5m��PE=5n��
��AB=CD+PC+DP+PE+EF+PF=12��m+n��=12��
��m+n=1��
��S�ı���CDFE=
��3m+3n����4m+4n����
=6��m+n��2
=6��
����DCP=��EPFʱ��
��DP=4m��PF=3n����CD=3m��EF=4n��
���ݹ��ɶ������ɵ�CP=5m��PE=5n��
��AB=12��m+n��=12��
��m+n=1��
��m��0��n��0��
��S�ı���CDFE=
��3m+4n����4m+3n��
=
(12m2+25mn+12n2)=
[12(m+n)2+mn]
=
��12+mn��
=6+
mn��6��
�����������ı���CDFE���������СֵΪ6��
�ߡ�CDP�͡�EFP���ǵ���ֱ�������Σ��ҡ�CDP=��EFP=90�㣬
��CD=DP=x��EF=PF=y��PC=
| 2 |
| 2 |
��AB=AP+PB=CD+DP+PC+PF+EF+PE
=x+x+
| 2 |
| 2 |
=��2+
| 2 |
��DF=2��
��x+y=2��
��AB=��2+
| 2 |
| 2 |
��2������CE��
����tan��C=
| 4 |
| 3 |
�ٵ���DCP=��PEFʱ��
��DP=4m��PF=4n����CD=3m��EF=3n��
���ݹ��ɶ������ɵ�CP=5m��PE=5n��

��AB=CD+PC+DP+PE+EF+PF=12��m+n��=12��
��m+n=1��
��S�ı���CDFE=
| 1 |
| 2 |
=6��m+n��2
=6��
����DCP=��EPFʱ��
��DP=4m��PF=3n����CD=3m��EF=4n��
���ݹ��ɶ������ɵ�CP=5m��PE=5n��
��AB=12��m+n��=12��
��m+n=1��
��m��0��n��0��
��S�ı���CDFE=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=6+
| 1 |
| 2 |
�����������ı���CDFE���������СֵΪ6��
������������Ҫ�����������ε��ۺ�Ӧ���Լ����ɶ���Ӧ�ã�������C��D��PΪ����������κ���E��F��PΪ��������������ƽ��з������۵ó��ǽ���ؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
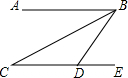 ��2007•��������ģ����ͼ��BCƽ�֡�ABD��AB��CD����E��CD���ӳ����ϣ�����C=28�㣬���BDE�Ķ���Ϊ��������
��2007•��������ģ����ͼ��BCƽ�֡�ABD��AB��CD����E��CD���ӳ����ϣ�����C=28�㣬���BDE�Ķ���Ϊ��������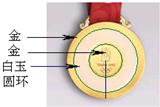 ��2007•��������ģ���������˻���ƴ����Եؽ�����Բ��Ƕ�����У���ͼ������һ��Ʋ����ǶԻ�ʤ�ߵ����ޣ�Ҳ�����ڹ�����л������Թ������ԡ��ȡ��¡��ļ�ֵ�ۣ�������Բ�������������������ı�ֵΪk�������и�����k��ӽ����ǣ�������
��2007•��������ģ���������˻���ƴ����Եؽ�����Բ��Ƕ�����У���ͼ������һ��Ʋ����ǶԻ�ʤ�ߵ����ޣ�Ҳ�����ڹ�����л������Թ������ԡ��ȡ��¡��ļ�ֵ�ۣ�������Բ�������������������ı�ֵΪk�������и�����k��ӽ����ǣ������� ��2007•��������ģ���á��衱����һ�����㣺��������ʵ��m��n��������y=ax2����y=ax2�裨m��n���ɵõ�y=a��x-m��2+n�����磺��y=3x2�裨2��4����õ�y=3��x-2��2+4��������y=x2�裨1��n����õ����º�����ͼ����ͼ��ʾ������n=
��2007•��������ģ���á��衱����һ�����㣺��������ʵ��m��n��������y=ax2����y=ax2�裨m��n���ɵõ�y=a��x-m��2+n�����磺��y=3x2�裨2��4����õ�y=3��x-2��2+4��������y=x2�裨1��n����õ����º�����ͼ����ͼ��ʾ������n=