题目内容
在第一次中考模拟考试中，初三级共有245名同学获得了数学科组的表扬．其中，被授予“数学精英”称号的人数是获得“超越自我”奖人数的8倍还多2人，求两个奖项各有多少人获得．
【答案】分析：设出获得“超越自我”奖为x人，根据授予“数学精英”称号的人数是获得“超越自我”奖人数的8倍还多2人，利用x表示出授予“数学精英”称号的人数，根据初三级共有245名同学获得了数学科组的表扬，列出关于x的一元一次方程，求出方程的解即为获得“超越自我”奖的人数，即可求出授予“数学精英”称号的人数．
解答：解：设获得“超越自我”奖为x人，则授予“数学精英”称号的人为（8x+2）人，
根据题意得：x+（8x+2）=245，即9x=243，
解得x=27，所以8x+2=218（人），
答：授予“数学精英”称号的人有218人，获得“超越自我”奖人有27人．
点评：此题考查学生会根据题中的等量关系列出相应的方程，是一道中档题．
解答：解：设获得“超越自我”奖为x人，则授予“数学精英”称号的人为（8x+2）人，
根据题意得：x+（8x+2）=245，即9x=243，
解得x=27，所以8x+2=218（人），
答：授予“数学精英”称号的人有218人，获得“超越自我”奖人有27人．
点评：此题考查学生会根据题中的等量关系列出相应的方程，是一道中档题．
练习册系列答案
相关题目
19、在本学期第九周进行的白云区08年初三毕业班中考第一次模拟考试（简称初三“一模”）中，九年级某班50名同学选择题（共10小题，每小题3分，满分30分）的得分情况如下表：
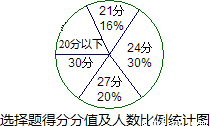
在本学期第九周进行的白云区08年初三毕业班中考第一次模拟考试（简称初三“一模”）中，九年级某班50名同学选择题（共10小题，每小题3分，满分30分）的得分情况如下表：
选择题得分分值及人数统计表
（1）该班选择题中，答对3题的人数为______人；
（2）该班选择题得分的平均分为______，众数为______，中位数为______；
（3）为了制作右面的扇形统计图（如图），请分别求出得20分以下人数占总人数的百分比及得满分人数的扇形圆心角度数，并补全该扇形统计图．
选择题得分分值及人数统计表
| 分 值 | 6 | 12 | 18 | 21 | 24 | 27 | 30 |
| 人 数 | 1 | 2 | 6 | 8 | 15 | 10 | 8 |
（2）该班选择题得分的平均分为______，众数为______，中位数为______；
（3）为了制作右面的扇形统计图（如图），请分别求出得20分以下人数占总人数的百分比及得满分人数的扇形圆心角度数，并补全该扇形统计图．