Question

【题目】如图，直线y=﹣x+3交y轴于点A，交x轴与点B，抛物线y=﹣x2+bx+c经过点A和点B，点P为抛物线上直线AB上方部分上的一点，且点P的横坐标为t，过P作PE∥x轴交直线AB于，作PH⊥x轴于H，PH交直线AB于点F．

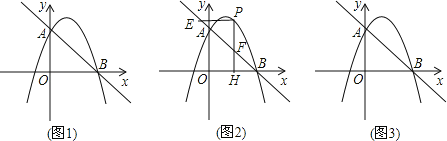
（1）求抛物线解析式；

（2）若PE的长为m，求m关于t的函数关系式；

（3）是否存在这样的t值，使得∠FOH﹣∠BEH=45°？若存在，求出t值，并求tan∠BEH的值，若不存在，请说明理由．

Answer 1

【答案】（1）抛物线解析式为y=﹣x2+2x+3；（2）m与t的关系式为m=﹣t2+3t；（3）存在满足条件的t的值，t的值为1，tan∠BEH的值为．

【解析】

试题分析：（1）由直线AB的解析式可求得A、B两点的坐标，代入抛物线解析式可求得b、c，可求得抛物线解析式；

（2）由P点坐标表示出E点的纵坐标，代入直线AB解析式，可求得E点横坐标，则可用t表示出PE的长，可得到m关于t的函数关系式；

（3）过E作EG⊥x轴于点G，则可用t表示出GH和EG，由三角形外角的性质和已知条件可证得∠EHG=∠FOH，可证明△FOH∽△EHG，根据相似三角形的性质可求得t的值，则可求得tan∠EHG，结合∠BEH=∠FOH﹣45°，则可求得tan∠BEH的值．

解：（1）在直线y=﹣x+3中，令x=0可得y=3，令y=0可得x=3，

∴A（0，3），B（3，0），

∵抛物线y=﹣x2+bx+c过A、B两点，

∴把A、B两点的坐标代入可得，解得，

∴抛物线解析式为y=﹣x2+2x+3；

（2）∵P点在抛物线上，

∴P点坐标为（t，﹣t2+2t+3），

∵PE∥x轴，

∴E点纵坐标为﹣t2+2t+3，

∵E点在直线AB上，

∴把E点纵坐标代入直线AB解析式可得﹣t2+2t+3=﹣x+3，解得x=t2﹣2t，

∴E点横坐标为t2﹣2t，

∴PE=m=t﹣（t2﹣2t）=﹣t2+3t，

∴m与t的关系式为m=﹣t2+3t；

（3）如图，过E作EG⊥x轴于点G，

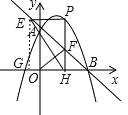
∵OA=OB=3，

∴∠EBO=45°，

∴∠EHG=∠BEH+∠EBO=∠EBH+45°，

∵∠FOH﹣∠BEH=45°，

∴∠FOH=∠BEH+45°，

∴∠EHG=∠FOH，且∠FHO=∠EGH=90°，

∴△FOH∽△EGH，

∴=，

∵OH=t，F在直线AB上，

∴FH=﹣t+3，

由（2）可知EG=﹣t2+2t+3，GH=m=﹣t2+3t，

∴=，解得t=1，

∴OH=1，FH=2，

∴tan∠FOH==2，

∵∠FOH﹣∠BEH=45°，

∴∠BEH=∠FOH﹣45°，

∴tan∠BEH=tan（∠FOH﹣45°）===，

综上可知存在满足条件的t的值，t的值为1，tan∠BEH的值为．