题目内容
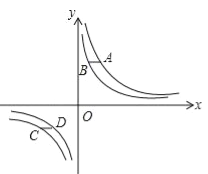
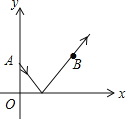
【题目】如图，从点
发出一束光，经x轴反射，过点
，则这束光从点A到点B所经过的路径的长为________.
【答案】５
【解析】
先过点B作BD⊥x轴于D，再由A、B的坐标确定，即可得OA,BD,OD的长度，由题意可证得△AOC∽△BDC，根据相似三角形的对应边成比例，即可求解.
解：如图，
过点B作BD⊥x轴于D，
∵A（0，2），B（5，3），
∴OA=2，BD=3，OD=5，
由反射定律可得：∠ACO=∠BCD，
又∵∠AOC=∠BDC=90°
∴△AOC∽△BDC，
∴OA：BD=OC：DC=AC：BC=2：3，
∴OC=2，OD=3
在Rt△BCD中，CD=3，BD=３
∴BC＝
＝
又∵AC：BC=2：3
∴AC＝
∴AC+BC＝5
..故选：5.
练习册系列答案
阅读快车系列答案
相关题目
【题目】探究函数y=x+
（x＞0）与y=x+
（x＞0，a＞0）的相关性质．
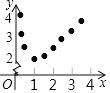
（1）小聪同学对函数y=x+（x＞0）进行了如下列表、描点，请你帮他完成连线的步骤；观察图象可得它的最小值为 ，它的另一条性质为 ；
x | … |
|
|
| 1 |
| 2 |
| 3 | … |
y | … |
|
|
| 2 |
|
|
|
| … |
（2）请用配方法求函数y=x+（x＞0）的最小值；
（3）猜想函数y=x+（x＞0，a＞0）的最小值为 ．
