题目内容
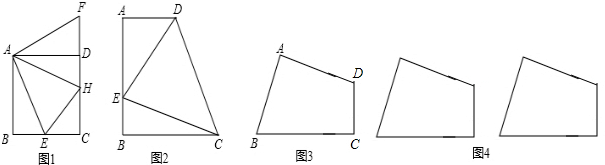
如图1，在正方形ABCD内有一点P满足AP=AB，PB=PC，连接AC、PD．（1）求证：△APB≌△DPC；
（2）求证：∠PAC=
∠BAP；（3）若将原题中的正方形ABCD变为等腰梯形ABCD（如图2），AD∥BC，且BA=AD=DC，形内一点P仍满足AP=AB，PB=PC，试问（2）中结论还成立吗？若成立请给予证明；若不成立，请说明理由．
【答案】分析：（1）根据全等三角形的判定定理可解．
（2）设∠PAC=x°，∠BAP=y°，可求出∠CAD=∠DCA=（60-x）°，∠PDC=y°，根据这个关系求出∠PAC=
∠BAP．
（3）以D为圆心，DA为半径画圆，连接各线，再求出各角之间的关系即可．
解答：解：（1）∵四边形ABCD为正方形，
∴∠ABC=∠DCB=90°，AB=CD，
∵BP=PC，
∴∠PBC=∠PCB，
∴∠ABP=∠DCP，
又∵AB=CD，BP=CP，
∴△ABP≌△DCP（SAS）．
（2）设∠PAC=x°，∠BAP=y°，则∠CAD=∠DCA=（60-x）°，∠PDC=y°．
由图形得，x+60=y+60-x，
∴y=2x，
∴∠PAC=
∠BAP．
（3）以D为圆心，DA为半径画圆，设∠PAC=x°，∠BAP=y°，
则∠CAD=∠DCA=（60-x）°，∠PDC=y°．
由图形得，x+60=y+60-x，
∴y=2x，
∴∠PAC=
∠BAP．
点评：本题难度较大，综合了全等三角形的判定定理，等腰梯形以及圆的有关知识．
（2）设∠PAC=x°，∠BAP=y°，可求出∠CAD=∠DCA=（60-x）°，∠PDC=y°，根据这个关系求出∠PAC=
∠BAP．（3）以D为圆心，DA为半径画圆，连接各线，再求出各角之间的关系即可．
解答：解：（1）∵四边形ABCD为正方形，
∴∠ABC=∠DCB=90°，AB=CD，
∵BP=PC，
∴∠PBC=∠PCB，
∴∠ABP=∠DCP，
又∵AB=CD，BP=CP，
∴△ABP≌△DCP（SAS）．
（2）设∠PAC=x°，∠BAP=y°，则∠CAD=∠DCA=（60-x）°，∠PDC=y°．由图形得，x+60=y+60-x，
∴y=2x，
∴∠PAC=
∠BAP．（3）以D为圆心，DA为半径画圆，设∠PAC=x°，∠BAP=y°，
则∠CAD=∠DCA=（60-x）°，∠PDC=y°．
由图形得，x+60=y+60-x，
∴y=2x，
∴∠PAC=
∠BAP．点评：本题难度较大，综合了全等三角形的判定定理，等腰梯形以及圆的有关知识．
练习册系列答案
阅读快车系列答案
相关题目
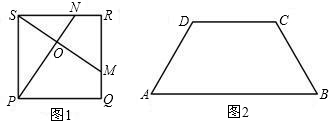构造一个与上述命题类似的正确命题并加以证明．
26、如图1，在正方形ABCD中，若点E是△DBC内的一点，且DE=DC，BE=CE．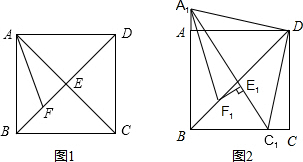
如图1，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F．