题目内容
【题目】如图,反比例函数y=![]() 的图象经过点(﹣1,-2
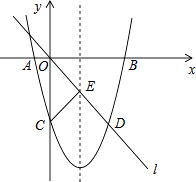
的图象经过点(﹣1,-2![]() ),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当
),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当![]() =
=![]() 时,则点C的坐标为 .
时,则点C的坐标为 . 
【答案】![]() (2,-
(2,-![]() )
)
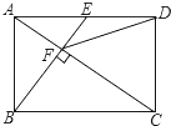
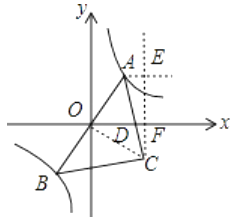
【解析】连接OC,作AE∥x轴、CE∥y轴,交于点E,连接CE交x轴于F点,如图:
依题可得A、B两点关于原点O对称,
∴OA=OB,
∵△ACB是以AB为斜边的等腰直角三角形,
∴OC=OA=OB,OC⊥AB,
设直线AB解析式为:y=cx(c![]() 0),则直线OC的解析式为:y=-
0),则直线OC的解析式为:y=-![]() x,
x,
∴设A(m,cm)(m> 0),则B(-m,-cm),
∵C在第四象限,
∴C(cm,-m),
又∵AE∥x轴、CE∥y轴,
∴△CAE∽△CDF,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,AC=AD+CD,
,AC=AD+CD,
∴![]() =
=![]() =
=![]() ,
,
∴E(cm,cm),F(cm,0),
∴![]() =
=![]() =
=![]() ,
,
∴c=![]() ,
,
∴A(m,![]() m)在反比例函数上,
m)在反比例函数上,
又∵(-1,-2![]() )在反比例函数上,
)在反比例函数上,
∴k=(-1)×(-2![]() )=2
)=2![]() ,
,
∴2![]() =
=![]() m2,
m2,
∵m> 0,
∴m=![]() ,
,
∴C(2,-![]() ).
).
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

练习册系列答案
相关题目