Question

【题目】如图，在平面直角坐标系xOy中，二次函数y=a（x+）（x﹣3）的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点M的纵坐标为－4．

（1）求出二次函数的解析式；

（2）如图1，若过点M作直线MN∥y轴，点P是直线MN上的一个动点，当PA+PC最小时，求点P的坐标.

（3）如图2，连结BC，在直线BC下方的抛物线上有一动点E，求△BCE面积的最大值.

Answer 1

【答案】（1）y=x2-x-3；（2）P(,-2)；（3）

【解析】

（1）由二次函数y=a（x+）（x﹣3）可求出A,B的坐标分别为（-，0），（3，0），从而求出二次函数y=a（x+）（x﹣3）的对称轴为x=，所点M的坐标为（，-4），把点M（，-4）代入y=a（x+）（x﹣3）即可求出a的值，从而得到二次函数解析式.

（2）如图1，依题意可知，MN即为二次函数的对称轴，所以连接BC，与MN的交点即为点P，先求直线BC的解析式，再令x=,求出对应的y的值即可.

（3）如图2所示，过点E作EF⊥AB于点F,则△BCE的面积=梯形OCEF的面积+△BEF的面积-△BCO的面积，设点E的坐标为（x, x2-x-3）,因为点E在BC下方，所以x的取值范围是0<x<3,根据等量关系式列式求解即可.

解：（1）依题意得：

A（-，0），B（3，0），

∴二次函数y=a（x+）（x﹣3）的对称轴为x=，

∵顶点M的纵坐标为－4

∴M（，-4）.

∴-4=a(+）（﹣3）

解得：a=.

∴二次函数解析式为y=x2-x-3；

（2）如图所示，

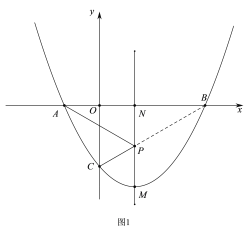
由于A,C在MN的同侧，要在MN上找一点P，使PA+PC的值最小，先找到A点关于MN的对称点B，再连接BC，BC与MN相交于点 P，此时P即为所求.

由（1）可知二次函数解析式为y=x2-x-3；B（3，0），

令x=0，则y=-3,故点C的坐标为（0，-3）

设直线BC的解析式为y=kx+b,则地

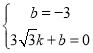
解得：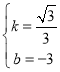

∴直线BC的解析式为y=x-3.

令x=，则y=-3=-2.

故点P的坐标为P(,-2)；

（3）如图2所示，过点E作EF⊥AB于点F, 设点E的坐标为（x, x2-x-3）,因为点E在BC下方，所以x的取值范围是0<x<3,

∴OF=x,EF=-x2+x+3,BF=<3-x.

∵OC=3,

∴△BCE的面积=梯形OCEF的面积+△BEF的面积-△BCO的面积

= (3-x2+x+3)x+ (-x2+x+3)( <3-x)- <33

= - + ++(- )+3x+ +---

= +(- )

=- +

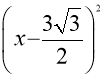∴当x= 时，△BCE的面积有最大值为.