题目内容
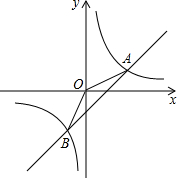
如图,函数y=
和y=
x的图象相交于A、B两点,其中点A的横坐标为2.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)在x轴上是否存在点P,使△BOP为等腰三角形?若存在,把符合条件的点P都求出来;若不存在,请说明理由.

| k |
| 2x |
| 1 |
| 2 |
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)在x轴上是否存在点P,使△BOP为等腰三角形?若存在,把符合条件的点P都求出来;若不存在,请说明理由.

(1)∵A为两函数图象的交点,A点横坐标为2,把A点的横坐标代入y=
x得,y=
×2=1,
∴A(2,1),
设反比例函数的解析式为y=
(k≠0),把A(2,1)代入得,
1=
,k=2,
∴反比例函数的解析式为y=
;(3分)
(2)由
,
解得
,
,
所以点B的坐标为:(-2,-1).(5分)
解法二:由对称性,A与B关于点O对称;
∵A(2,1),∴B(-2,-1)(5分)
(3)作BC⊥x轴,垂足为C,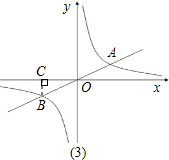
∵B(-2,-1),∴OC=2,BC=1,
在Rt△OBC中,由勾股定理得,
OB=
=
=
.(6分)
分三种情况讨论:
①当OB=OP时,P1(
,0),P2(-
,0);(8分)
②当OB=BP3时,OP3=2OC=4,∴P3(-4,0).(9分)
③作OB的垂直平分线交OB于D.
设P4(x,0),则OP4=BP4=-x,CP4=2+x,BC=1.
(2+x)2+12=(-x)2,
x=-
∴p4(-
,0),(11分)
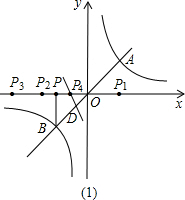
综上所述,符合条件的P点坐标为:
P1(
,0)、P2(-
,0)、P3(-4,0)、p4(-
,0).(12分)
| 1 |
| 2 |
| 1 |
| 2 |
∴A(2,1),
设反比例函数的解析式为y=
| k |
| x |
1=
| k |
| 2 |
∴反比例函数的解析式为y=
| 2 |
| x |
(2)由
|
解得
|
|
所以点B的坐标为:(-2,-1).(5分)
解法二:由对称性,A与B关于点O对称;
∵A(2,1),∴B(-2,-1)(5分)
(3)作BC⊥x轴,垂足为C,

∵B(-2,-1),∴OC=2,BC=1,
在Rt△OBC中,由勾股定理得,
OB=
| OC2+BC2 |
| 12+22 |
| 5 |
分三种情况讨论:
①当OB=OP时,P1(
| 5 |
| 5 |
②当OB=BP3时,OP3=2OC=4,∴P3(-4,0).(9分)
③作OB的垂直平分线交OB于D.
设P4(x,0),则OP4=BP4=-x,CP4=2+x,BC=1.
(2+x)2+12=(-x)2,
x=-
| 5 |
| 4 |
| 5 |
| 4 |
综上所述,符合条件的P点坐标为:
P1(
| 5 |
| 5 |
| 5 |
| 4 |


练习册系列答案
相关题目