题目内容
已知:△ABC中,AB=AC,AD⊥BC于D.
(1)如图(1),若点M在线段AD上(点M不与点A重合),则∠AMB
(2)如图2,若点M在线段BD上(点M不与点B,D重合),点N在线段CD上且ND=MD,则∠AMB
(3)如图3,若点M在△ABD的内部,是比较∠AMB与∠AMC的大小,并证明你的结论.

(1)如图(1),若点M在线段AD上(点M不与点A重合),则∠AMB
=
=
∠AMC(请填>,=或<);(2)如图2,若点M在线段BD上(点M不与点B,D重合),点N在线段CD上且ND=MD,则∠AMB
=
=
∠ANC,∠AMC<
<
∠ANC(请填>,=或<);(3)如图3,若点M在△ABD的内部,是比较∠AMB与∠AMC的大小,并证明你的结论.

分析:(1)根据等腰三角形三线合一的性质可得∠BAM=∠CAM,然后证明△ABM与△ACM全等,根据全等三角形对应角相等即可证明;
(2)利用边角边证明△ADM与△ADN全等,然后根据全等三角形对应角相等得到∠AMD=∠AND,再根据等角的补角相等即可得证;根据三角形的锐角小于相邻的外角解答;
(3)先找出点M关于AD的对称点N,然后连接AN,MN,CN,延长CN交AM于点P,根据对称性可得△ABM与△ACN全等,根据全等三角形对应角相等得到∠1=∠2,再根据三角形的一个外角大于与它不相邻的任何以一个内角即可推出.
(2)利用边角边证明△ADM与△ADN全等,然后根据全等三角形对应角相等得到∠AMD=∠AND,再根据等角的补角相等即可得证;根据三角形的锐角小于相邻的外角解答;
(3)先找出点M关于AD的对称点N,然后连接AN,MN,CN,延长CN交AM于点P,根据对称性可得△ABM与△ACN全等,根据全等三角形对应角相等得到∠1=∠2,再根据三角形的一个外角大于与它不相邻的任何以一个内角即可推出.
解答:解:(1)∵AB=AC,AD⊥BC于D,
∴∠BAM=∠CAM(等腰三角形三线合一),
在△ABM与△ACM中,
,
∴△ABM≌△ACM(SAS),
∴∠AMB=∠AMC;
(2)∵AD⊥BC,
∴∠ADM=∠ADN=90°,
在△ADM与△ADN中,
,
∴△ADM≌△ADN(SAS),
∴∠AMD=∠AND,
∴180°-∠AMD=180°-∠AND,
即∠AMB=∠ANC,
在Rt△ADN中,∠AND是锐角,
∴∠AND<∠ANC,
∴∠AMC<∠ANC;
(3)如图,作点M关于AD的对称点N,连接AN,CN,延长CN交AM于点P,
∵AB=AC,AD⊥BC于D,
∴AD垂直平分BC,
∴点B、C关于AD所在的直线对称,
∴△ABM≌△ACN,
∴∠1=∠2,
∵∠2是△APN的外角,
∴∠2>∠3,
∵∠3是△PMC的外角,
∴∠3>∠PMC,
∴∠1>∠PMC,
即∠AMB>∠AMC.
故答案为:(1)=;(2)=,<;(3)∠AMB>∠AMC.
∴∠BAM=∠CAM(等腰三角形三线合一),
在△ABM与△ACM中,
|
∴△ABM≌△ACM(SAS),
∴∠AMB=∠AMC;
(2)∵AD⊥BC,
∴∠ADM=∠ADN=90°,
在△ADM与△ADN中,
|
∴△ADM≌△ADN(SAS),
∴∠AMD=∠AND,
∴180°-∠AMD=180°-∠AND,
即∠AMB=∠ANC,
在Rt△ADN中,∠AND是锐角,
∴∠AND<∠ANC,
∴∠AMC<∠ANC;
(3)如图,作点M关于AD的对称点N,连接AN,CN,延长CN交AM于点P,
∵AB=AC,AD⊥BC于D,
∴AD垂直平分BC,
∴点B、C关于AD所在的直线对称,

∴△ABM≌△ACN,
∴∠1=∠2,
∵∠2是△APN的外角,
∴∠2>∠3,
∵∠3是△PMC的外角,
∴∠3>∠PMC,
∴∠1>∠PMC,
即∠AMB>∠AMC.
故答案为:(1)=;(2)=,<;(3)∠AMB>∠AMC.
点评:本题主要考查了三角形的一个外角大于与它不相邻的任何以一个内角的性质,全等三角形的判定与性质,作出辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
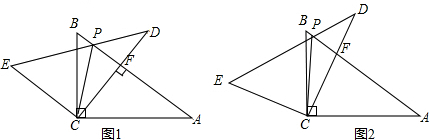
 如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示)
如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示) 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.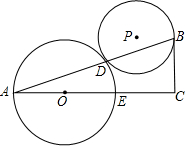 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,