��Ŀ����
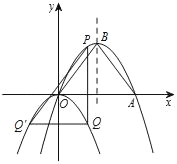
����Ŀ����ͼ��������y=��![]() x2+bx+c����ԭ��͵�A��6��0��������Գ��ύ�ڵ�B��P��������y=��
x2+bx+c����ԭ��͵�A��6��0��������Գ��ύ�ڵ�B��P��������y=��![]() x2+bx+c��һ���㣬����x���Ϸ�������P��x��Ĵ��߽���������y=��
x2+bx+c��һ���㣬����x���Ϸ�������P��x��Ĵ��߽���������y=��![]() ��x��h��2��hΪ�������ڵ�Q������Q��PQ�Ĵ��߽���������y=��
��x��h��2��hΪ�������ڵ�Q������Q��PQ�Ĵ��߽���������y=��![]() ��x��h��2�ڵ�Q���������Q�غϣ�������PQ�������P�ĺ�����Ϊm��
��x��h��2�ڵ�Q���������Q�غϣ�������PQ�������P�ĺ�����Ϊm��
��1����������y=��![]() x2+bx+c�ĺ�����ϵʽ����B�����ꣻ
x2+bx+c�ĺ�����ϵʽ����B�����ꣻ
��2����h=0ʱ��
����֤�� ![]() ��
��
������PQQ������OAB�ص�����ͼ�ε��ܳ�Ϊl����l��m֮��ĺ�����ϵʽ��
��3����h��0ʱ���Ƿ���ڵ�P��ʹ�ı���OAQQ��Ϊ���Σ������ڣ���ֱ��д��h��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() ��x��3��2+4����B������Ϊ��3��4������2����֤����������l=
��x��3��2+4����B������Ϊ��3��4������2����֤����������l= ��3�����ڣ�h=3��2
��3�����ڣ�h=3��2![]() ��3+2
��3+2![]() ʱ���ı���OAQQ��Ϊ����
ʱ���ı���OAQQ��Ϊ����
�������������������1���ô���ϵ������ú�������ʽ���ѽ���ʽ��Ϊ����ʽ��ֱ��д����B�����꼴�ɣ���2���ٵ�h=0ʱ����������ߵĽ���ʽ����m��ʾ����P��Q������������m��ʾ��PQ��QQ���ij������㼴�ɵý��ۣ��ڷֵ�0��m��3ʱ�͵�3��m��6ʱ���������l��m֮��ĺ�����ϵʽ����3�����ڣ����ı���OQ��1Q1A������ʱ��OQ��1=OA=Q1Q��1=6��
�������ߵĶ�����ԭ��ʱ�������Q1�������Ϊ3����x=3����y=��![]() x2���� y=-4��������ƽ�ƣ���֪Q�������겻�䣬��RT��OHQ��1���У�OH=4��OQ��1=6�����ݹ��ɶ������HQ��1=2
x2���� y=-4��������ƽ�ƣ���֪Q�������겻�䣬��RT��OHQ��1���У�OH=4��OQ��1=6�����ݹ��ɶ������HQ��1=2![]() �����ɵ�h��ֵ(���ݺ����ĶԳ���).
�����ɵ�h��ֵ(���ݺ����ĶԳ���).
���������
��1����������y=��![]() x2+bx+c����0��0���͵�A��6��0��
x2+bx+c����0��0���͵�A��6��0��
��![]() ��
��
���![]() ��
��
��������y=��![]() x2+bx+c�ĺ�����ϵʽΪ��y=��
x2+bx+c�ĺ�����ϵʽΪ��y=��![]() x2+8x��
x2+8x��
��y=��![]() ��x��3��2+4��
��x��3��2+4��
����B��������3��4����
��2����֤������h=0ʱ��������Ϊy=��![]() x2��
x2��
��P��m����![]() m2+
m2+![]() m����Q��m����
m����Q��m����![]() m2����
m2����
��PQ=![]() m��QQ��=2m��
m��QQ��=2m��
��![]() =
=![]() =
=![]() ��
��
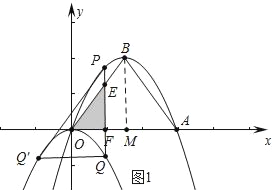
����ͼ1�У���0��m��3ʱ����PQ��OB���ڵ�E����OA���ڵ�F��
��![]() =
=![]() ����PQQ��=��BMO=90�㣬
����PQQ��=��BMO=90�㣬
���PQQ��ס�BMO��
���QPQ��=��OBM��
��EF��BM��
���OEF=��OBM��
���OEF=��QPQ�䣬
��OE��PQ�䣬
��![]() =
=![]() ��
��
��EF=![]() ��OE=
��OE=![]() ��
��
��l=OF+EF+OE=m+![]() +
+![]() m=4m��
m=4m��
��3��m��6ʱ����ͼ2�У���PQ����AB���ڵ�H����x�ύ�ڵ�G��PQ��AB��E����OA��F����HM��OA��M��

��AF=6��m��tan��EAF=![]() =
=![]() ��
��
��EF=![]() ��6��m����AE=
��6��m����AE=![]() ��
��
��tan��PGF=![]() =
=![]() ��PF=��
��PF=��![]() x2+
x2+![]() x��
x��
��GF=��![]() m2+2m��
m2+2m��
��AG=��![]() m2+m+6��
m2+m+6��
��GM=AM=��![]() m2+
m2+![]() m+3��
m+3��
��HG=HA=![]() =��
=��![]() m2+
m2+![]() m+5��
m+5��
��l=GH+EH+EF+FG=��![]() m2+4m+8��
m2+4m+8��
��������l= ��
��
��3����ͼ3�У����ڣ�
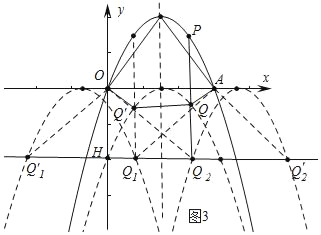
���ı���OQ��1Q1A������ʱ��OQ��1=OA=Q1Q��1=6��
��������ԭ��ʱ��Q1�������Ϊ3����x=3����
y=��![]() x2���� y=-4��������ƽ�ƣ�Q�������겻�䣬
x2���� y=-4��������ƽ�ƣ�Q�������겻�䣬
����Q1��������Ϊ-4��
��RT��OHQ��1����OH=4��OQ��1=6��
��HQ��1=2![]() ��
��
��h=3��2![]() ��3+2
��3+2![]() ��
��
��������h=3��2![]() ��3+2
��3+2![]() ʱ���ı���OAQQ��Ϊ���Σ�
ʱ���ı���OAQQ��Ϊ���Σ�

 A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д� ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д�