题目内容
 如图,直角坐标系中,O为原点,等腰△AOB的顶点B在x轴上,AO=AB,反比例函数y=
如图,直角坐标系中,O为原点,等腰△AOB的顶点B在x轴上,AO=AB,反比例函数y= (k>0)在第一象限内的图象经过AB的中点C,若△AOB的面积是12,则k的值是
(k>0)在第一象限内的图象经过AB的中点C,若△AOB的面积是12,则k的值是
- A.4.5
- B.6
- C.9
- D.12
C
分析:分别过点A、点C作OB的垂线,垂足分别为点D、点C,根据等腰三角形的性质得OD=BD,而点C为AB的中点,利用三角形中位线的性质得到ED=BE,CE= AD,则OE=
AD,则OE= OB,再根据三角形的面积公式得到
OB,再根据三角形的面积公式得到 AD•OB=12,易得CE•OE=9,设C点坐标为(x,y),即可得到k=xy=CE•OE=9.
AD•OB=12,易得CE•OE=9,设C点坐标为(x,y),即可得到k=xy=CE•OE=9.
解答: 解:分别过点A、点C作OB的垂线,垂足分别为点D、点C,如图,
解:分别过点A、点C作OB的垂线,垂足分别为点D、点C,如图,
∵AO=AB,
∴OD=BD,
又∵点C为AB的中点,
且CE∥AD,
∴CE为△ADE的中位线,
∴ED=BE,CE= AD,
AD,
∴OE= OB,
OB,
∵△AOB的面积是12,
∴ AD•OB=12,
AD•OB=12,
∴CE• OE=12,
OE=12,
∴CE•OE=9,
设C点坐标为(x,y),而点C在反比例函数y= (k>0)的图象上,
(k>0)的图象上,
∴k=xy=CE•OE=9.
故选C.
点评:本题考查了确定反比例函数y= (k≠0)的k值的方法:通过几何方法得到其图象上某点的横纵坐标之积即可.也考查了等腰三角形的性质以及三角形中位线的性质.
(k≠0)的k值的方法:通过几何方法得到其图象上某点的横纵坐标之积即可.也考查了等腰三角形的性质以及三角形中位线的性质.
分析:分别过点A、点C作OB的垂线,垂足分别为点D、点C,根据等腰三角形的性质得OD=BD,而点C为AB的中点,利用三角形中位线的性质得到ED=BE,CE=
 AD,则OE=
AD,则OE= OB,再根据三角形的面积公式得到
OB,再根据三角形的面积公式得到 AD•OB=12,易得CE•OE=9,设C点坐标为(x,y),即可得到k=xy=CE•OE=9.
AD•OB=12,易得CE•OE=9,设C点坐标为(x,y),即可得到k=xy=CE•OE=9.解答:
 解:分别过点A、点C作OB的垂线,垂足分别为点D、点C,如图,
解:分别过点A、点C作OB的垂线,垂足分别为点D、点C,如图,∵AO=AB,
∴OD=BD,
又∵点C为AB的中点,
且CE∥AD,
∴CE为△ADE的中位线,
∴ED=BE,CE=
 AD,
AD,∴OE=
 OB,
OB,∵△AOB的面积是12,
∴
 AD•OB=12,
AD•OB=12,∴CE•
 OE=12,
OE=12,∴CE•OE=9,
设C点坐标为(x,y),而点C在反比例函数y=
 (k>0)的图象上,
(k>0)的图象上,∴k=xy=CE•OE=9.
故选C.
点评:本题考查了确定反比例函数y=
 (k≠0)的k值的方法:通过几何方法得到其图象上某点的横纵坐标之积即可.也考查了等腰三角形的性质以及三角形中位线的性质.
(k≠0)的k值的方法:通过几何方法得到其图象上某点的横纵坐标之积即可.也考查了等腰三角形的性质以及三角形中位线的性质. 
练习册系列答案
相关题目
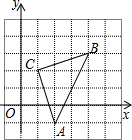 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,A点坐标为(2,-1),则△ABC的面积为 ?若存在,请求出所有这样的点;若不存在,请说明理由.
?若存在,请求出所有这样的点;若不存在,请说明理由. 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4), 如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是
如图,直角坐标系中,△ABC的顶点都在网格点上,C点坐标为(1,2),原来△ABC各个顶点纵坐标不变,横坐标都增加2,所得的三角形面积是 在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示:
在如图的直角坐标系中,将△ABC平移后得到△A′B′C′,它们的个顶点坐标如表所示: