Question

如图，等腰梯形ABCD中，E为CD的中点，EF⊥AB于F，如果AB=6，EF=5，求梯形ABCD的面积．

Answer 1

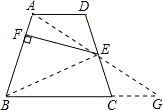解：如图，连接AE交BC的延长线于G点，连接BE．
∵AD∥BG，
∴∠DAE=∠G，∠D=∠DCG，又DE=EC，
∴△ADE≌△GCE，
∴AE=GE，
∴S_△ABE=S_△GBE，
则S_△ABG=S_梯形ABCD=2S_△ABE=2×15=30．
分析：连接AE交BC的延长线于G点，根据两直线平行得到两对内错角相等，再由E为中点得到一对边对应相等，从而得到三角形ADE与三角形GCE全等，由全等三角形的对应边相等得到AE=GE，根据E为AG中点，利用等底同高即可得到三角形ABE与三角形BEG面积相等，则梯形ABCD的面积就是△ABE的面积的2倍，则问题就可以比较容易求解．
点评：已知梯形的腰的中点时，本题的辅助线的作法是需要熟记的．