题目内容
如图，正方形ABCD中，点P、点Q分别在BC、CD上，∠PAQ=45゜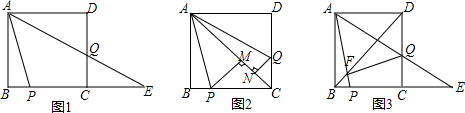
（1）如图1，若AQ交BC的延长线于E，若AB=4，BP=1，求PE；
（2）如图2，过P点作PM⊥AC，QN⊥AC，垂足分别为M、N，若AB=4，求AM•AN的值；
（3）如图3，若AP交BD于F点，连FQ，求证：AF=FQ．
（1）如图1，若AQ交BC的延长线于E，若AB=4，BP=1，求PE；
（2）如图2，过P点作PM⊥AC，QN⊥AC，垂足分别为M、N，若AB=4，求AM•AN的值；
（3）如图3，若AP交BD于F点，连FQ，求证：AF=FQ．
分析：（1）设CE=a，则PE=4-1+a=3+a，由勾股定理求出AP=
，过E作EH⊥AP交AP延长线于H，证△ABP∽△EHP，得出
=
=
，求出EH=
，HP=
，求出EH=AH=AP+PH，得出方程
=
+
，求出即可；
（2）证△ABP∽△ANQ，得出
=
，求出AN=
，同理证△AMP∽△ADQ，求出AM=
，代入求出即可；
（3）证△AOF∽∠DOQ，得出
=
，根据∠AOD=∠FOQ和比例式证△AOD∽△FOQ，推出∠5=∠6=45°，求出∠1=∠6，根据等腰三角形的判定推出即可．
| 17 |
| AB |
| EH |
| AP |
| PE |
| BP |
| PH |
| 4(3+a) | ||
|
| 3+a | ||
|
| 4(3+a) | ||
|
| 17 |
| 3+a | ||
|
（2）证△ABP∽△ANQ，得出
| AB |
| AP |
| AN |
| AQ |
| 4AQ |
| AP |
| 4AP |
| AQ |
（3）证△AOF∽∠DOQ，得出
| AO |
| DO |
| OF |
| OQ |
解答：
（1）解：设CE=a，则PE=4-1+a=3+a，
在Rt△ABP中，由勾股定理得：AP=
=
，
如图，过E作EH⊥AP交AP延长线于H，
∵四边形ABCD是正方形，
∴∠B=∠H=90°，
∵∠1=∠2，
∴△ABP∽△EHP，
∴
=
=
，
∴EH=
=
，HP=
=
，
∵∠H=90°，∠PAQ=45°，
∴∠HEA=45°=∠PAQ，
∴EH=AH=AP+PH，
∴
=
+
，
解得：a=
，
∴PE=3+a=
．
（2）解：
如图，∵四边形ABCD是正方形，
∴∠B=90°，∠BAC=45°=∠1+∠2，
∵∠PAQ=45°=∠2+∠3，
∴∠1=∠3，
∵QN⊥AC，
∴∠ANQ=∠B=90°，
∴△ABP∽△ANQ，
∴
=
，
∵AB=4，
∴AN=
，
同理△AMP∽△ADQ，
∴
=
，
∵AD=AB=4，
∴AM=
，
∴AM•AN=
•
=16．
（3）
证明：如图，∵∠PAQ=45°，四边形ABCD是正方形，
∴∠ADQ=90°，∠5=45°，∠1=∠2=45°，
∵∠3=∠4，
∴△AOF∽∠DOQ，
∴
=
，
∴
=
，
∵∠AOD=∠FOQ，
∴△AOD∽△FOQ，
∴∠6=∠5=45°，
∴∠1=∠6=45°，
∴AF=FQ．
（1）解：设CE=a，则PE=4-1+a=3+a，在Rt△ABP中，由勾股定理得：AP=
| 42+12 |
| 17 |
如图，过E作EH⊥AP交AP延长线于H，
∵四边形ABCD是正方形，
∴∠B=∠H=90°，
∵∠1=∠2，
∴△ABP∽△EHP，
∴
| AB |
| EH |
| AP |
| PE |
| BP |
| PH |
∴EH=
| AB•PE |
| AP |
| 4(3+a) | ||
|
| BP•PE |
| AP |
| 3+a | ||
|
∵∠H=90°，∠PAQ=45°，
∴∠HEA=45°=∠PAQ，
∴EH=AH=AP+PH，
∴
| 4(3+a) | ||
|
| 17 |
| 3+a | ||
|
解得：a=
| 8 |
| 3 |
∴PE=3+a=
| 17 |
| 3 |
（2）解：
如图，∵四边形ABCD是正方形，∴∠B=90°，∠BAC=45°=∠1+∠2，
∵∠PAQ=45°=∠2+∠3，
∴∠1=∠3，
∵QN⊥AC，
∴∠ANQ=∠B=90°，
∴△ABP∽△ANQ，
∴
| AB |
| AP |
| AN |
| AQ |
∵AB=4，
∴AN=
| 4AQ |
| AP |
同理△AMP∽△ADQ，
∴
| AD |
| AQ |
| AM |
| AP |
∵AD=AB=4，
∴AM=
| 4AP |
| AQ |
∴AM•AN=
| 4AP |
| AQ |
| 4AQ |
| AP |
（3）
证明：如图，∵∠PAQ=45°，四边形ABCD是正方形，∴∠ADQ=90°，∠5=45°，∠1=∠2=45°，
∵∠3=∠4，
∴△AOF∽∠DOQ，
∴
| AO |
| DO |
| OF |
| OQ |
∴
| AO |
| OF |
| DO |
| OQ |
∵∠AOD=∠FOQ，
∴△AOD∽△FOQ，
∴∠6=∠5=45°，
∴∠1=∠6=45°，
∴AF=FQ．
点评：本题考查了正方形性质，相似三角形的性质和判定，等腰三角形的性质和判定的应用，主要考查学生综合运用定理进行推理的能力，综合性比较强，难度偏大．
练习册系列答案
相关题目
19、如图：正方形ABCD，M是线段BC上一点，且不与B、C重合，AE⊥DM于E，CF⊥DM于F．求证：AE2+CF2=AD2．
如图，正方形ABCD中，E点在BC上，AE平分∠BAC．若BE=
如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③AG∥CF；④S△FGC=3．其中正确结论的个数是（ ）
17、如图，正方形ABCD的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角板的两条直角边与CD交于点F，与CB延长线交于点E，四边形AECF的面积是
如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接BE、DG．