题目内容
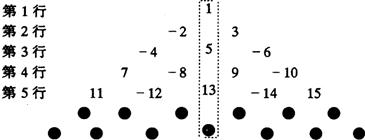
8、已知一列数:1,-2,3,-4,5,-6,7,…将这列数排成下列形式:中间用虚线围的一列数,从上至下依次为1,5,13,25…,按照上述规律排上去,那么虚线框中的第7个数是
85
.
分析:分析可得,第n行第一个数的绝对值为$\frac{n•(n-1)}{2}$,且奇数为正,偶数为负;中间用虚线围的一列数,从上至下依次为1,5,13,25…,为奇数,且每n个数比前一个大4(n-1);故第7个数是85.
解答:解:∵中间用虚线围的一列数,从上至下依次为1,5,13,25…,为奇数,且每n个数比前一个大4(n-1),
∴第7个数是85.
∴第7个数是85.
点评:本题是一道找规律的题目,要求学生的通过观察,分析、归纳并发现其中的规律,并应用规律解决问题.本题的规律为第n行第一个数的绝对值为$\frac{n•(n-1)}{2}$,且奇数为正,偶数为负;中间用虚线围的一列数,从上至下依次为1,5,13,25…,为奇数,且每n个数比前一个大4(n-1).

练习册系列答案
相关题目
已知一列数:3,6,9,12,15,18…若将这列数的第一个数记为a1,第二个数记为a2…,第n个数记为an那么a1=3,a2=3+(2-1)×3,a3=3+(3-1)×3…根据上述规律,写出前n项的和Sn为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
