题目内容
在锐角△ABC中，∠B=30°，以A为圆心，AB长为半径作⊙A，以C为圆心，AC长为半径作⊙C，则⊙A与⊙C的位置关系为
- A.外切
- B.相交
- C.内切
- D.内含
B
分析：本题可画出图形，观察：⊙C过⊙A的圆心A，两圆相交．
解答：依题意得：如图所示，两圆相交．
故选B．
点评：此题考查的是两个圆之间的位置关系，解此类题目时可根据图形中的两个圆的交点个数来判断两个圆的位置关系．
分析：本题可画出图形，观察：⊙C过⊙A的圆心A，两圆相交．
解答：依题意得：如图所示，两圆相交．
故选B．
点评：此题考查的是两个圆之间的位置关系，解此类题目时可根据图形中的两个圆的交点个数来判断两个圆的位置关系．
练习册系列答案
相关题目
在锐角△ABC中，a、b、c分别表示为∠A、∠B、∠C的对边，O为其外心，则O点到三边的距离之比为（ ）
| A、a：b：c | ||||||
B、
| ||||||
| C、cosA：cosB：cosC | ||||||
| D、sinA：sinB：sinC |
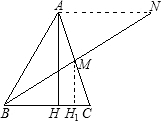在锐角△ABC中，最大的高线AH等于中线BM，求证：∠B＜60°（如图）．
如图，在锐角△ABC中，∠BAC=60°，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①B、E、D、C四点共圆；②AD•AC=AE•AB；③△DEF是等边三角形；④当∠ABC=45°时，BE=
（2013•南开区一模）在锐角△ABC中，∠BAC=60°，BD、CE为高，F是BC的中点，连接DE、EF、FD，则以下结论中一定正确的个数有（ ）