题目内容
抛物线y=x2-2x+3与坐标轴交点为（ ）A．二个交点
B．一个交点
C．无交点
D．三个交点
【答案】分析：由题意先分别判断抛物线与x轴和y轴的交点个数，令y=0，看方程是否有解，然后再令x=0，求出与y轴的交点，从而求解．
解答：解：令y=0得方程，
x2-2x+3=0，
△=（-2）2-4×1×3＜0，
∴方程无解，
∴抛物线y=x2-2x+3与x轴交点为0个，
又∵当x=0时，y=3，
∴抛物线交y轴于点（0，3），
∴抛物线y=x2-2x+3与坐标轴交点为一个；
故选B．
点评：此题主要考查抛物线的性质及图象，把抛物线同方程联系起来命题，是常见的题型．
解答：解：令y=0得方程，
x2-2x+3=0，
△=（-2）2-4×1×3＜0，
∴方程无解，
∴抛物线y=x2-2x+3与x轴交点为0个，
又∵当x=0时，y=3，
∴抛物线交y轴于点（0，3），
∴抛物线y=x2-2x+3与坐标轴交点为一个；
故选B．
点评：此题主要考查抛物线的性质及图象，把抛物线同方程联系起来命题，是常见的题型．
练习册系列答案
相关题目
抛物线y=x2+2x-2的图象上最低点的坐标是（ ）
| A、（2，-2） | B、（1，-2） | C、（1，-3） | D、（-1，-3） |
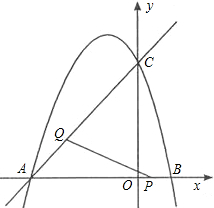秒，请求出△APQ的面积S与t的函数关系式，并求出当t为何值时，△APQ的面积最大，最大面积是多少？