��Ŀ����
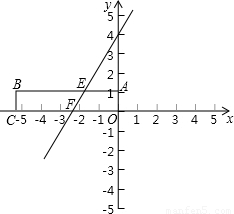
��2010•�ߺ�����ͼ����ƽ��ֱ������ϵ�з���һ����ABCO���䶥��ΪA��0��1����B��-3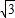 ��1����C��-3
��1����C��-3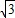 ��0����O��0��0�������˾������Ź�E��-
��0����O��0��0�������˾������Ź�E��-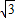 ��1����F��-
��1����F��-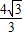 ��0����ֱ��EF�����·����ۣ�B��C�Ķ�Ӧ��ֱ�ΪB�䡢C�䣮
��0����ֱ��EF�����·����ۣ�B��C�Ķ�Ӧ��ֱ�ΪB�䡢C�䣮��1�����ۺ�����ֱ��EF�Ľ���ʽ��
��2��һ�����߾���B��E��B�����㣬��˶��κ�������ʽ��
��3���ܷ���ֱ��EF����һ��P��ʹ�á�PBC�ܳ���С�����ܣ������P�����ꣻ�����ܣ�˵�����ɣ�
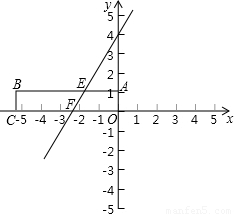
���𰸡���������1������E��F�����꣬���ֱ��ʽEF�Ľ���ʽΪy=kx+b������������룬���k��b���ɣ�
��2����B����B��A���BA��A�䣬��Rt��B��EA���У�ͨ����ֱ�������ο����A��E��A��B��ij���ͨ��֤A��E=AE���ó�B����y���ϵĽ��ۣ��Ӷ��ó�B�����꣬�����ô���ϵ������������ߵĽ���ʽ��
��3������B��C������B��B�����EF����ֱ�߶Գƣ���B��C���ۺ۵Ľ��㼴Ϊ�����P�㣬�����ֱ��B��C�Ľ���ʽ�������ۺ�EF�Ľ���ʽ�������P�����꣮
����⣺��1�������ۺ�����ֱ��EF��E��- ��1����F��-
��1����F��- ��0��������
��0��������
����ֱ��EF�Ľ���ʽΪy=kx+b��
�� ��
��
���k= ��b=4��
��b=4��
����ֱ��EF�Ľ���ʽΪ��y= x+4��
x+4��
��2���������ֱ��EF�����·����ۺ�B��C�Ķ�Ӧ��ΪB�䣨x1��y1����C�䣨x2��y2����
��B����B��A���AE��AE����ֱ����A��㣻
��B��E=BE=2 ����B��EF=��BEF=60°��
����B��EF=��BEF=60°��
���B��EA��=60°��
��A��E= ��B��A��=3��
��B��A��=3��
��A��A���غϣ�B����y���ϣ�
��x1=0��y1=-2��
��B�䣨0��-2��������ʱ��˵��B�䣨x1��y1����y���ϡ���
����κ�������ʽΪ��y=ax2+bx+c�������߹�B��-3 ��1����E��-
��1����E��- ��1����B�䣨0��-2����
��1����B�䣨0��-2����
�õ� ��
��
���
��ö��κ�������ʽy=- x2-
x2- x-2��
x-2��
��3���ܣ�������ֱ��EF���ҵ�P�㣻
����B��C��EF��P�㣬������BP��
����B��P=BP����ʱ��P��C��B����һ��ֱ���ϣ���BP+PC=B��P+PC�ĺ���С��
����BCΪ���������������PBC�ܳ���С��
��ֱ��B��C�Ľ���ʽΪ��y=kx+b�����У�
 ��
��
��� ��
��
��ֱ��B��C�Ľ���ʽΪ��y=- x-2��
x-2��
�֡�PΪֱ��B��C��ֱ��EF�Ľ��㣬
�� ��
��
��� ��
��
���P��������- ��-
��- ����
����
������������Ҫ������һ�κ��������κ�������ʽ��ȷ������Գ�ͼ�ε����ʡ�����ͼ���֪ʶ���Ѷ�ƫ��
��2����B����B��A���BA��A�䣬��Rt��B��EA���У�ͨ����ֱ�������ο����A��E��A��B��ij���ͨ��֤A��E=AE���ó�B����y���ϵĽ��ۣ��Ӷ��ó�B�����꣬�����ô���ϵ������������ߵĽ���ʽ��
��3������B��C������B��B�����EF����ֱ�߶Գƣ���B��C���ۺ۵Ľ��㼴Ϊ�����P�㣬�����ֱ��B��C�Ľ���ʽ�������ۺ�EF�Ľ���ʽ�������P�����꣮
����⣺��1�������ۺ�����ֱ��EF��E��-
 ��1����F��-
��1����F��- ��0��������
��0�������У�����ֱ��EF�Ľ���ʽΪy=kx+b��
��
 ��
�����k=
 ��b=4��
��b=4������ֱ��EF�Ľ���ʽΪ��y=
 x+4��
x+4����2���������ֱ��EF�����·����ۺ�B��C�Ķ�Ӧ��ΪB�䣨x1��y1����C�䣨x2��y2����
��B����B��A���AE��AE����ֱ����A��㣻
��B��E=BE=2
 ����B��EF=��BEF=60°��
����B��EF=��BEF=60°��
���B��EA��=60°��
��A��E=
 ��B��A��=3��
��B��A��=3����A��A���غϣ�B����y���ϣ�
��x1=0��y1=-2��
��B�䣨0��-2��������ʱ��˵��B�䣨x1��y1����y���ϡ���
����κ�������ʽΪ��y=ax2+bx+c�������߹�B��-3
 ��1����E��-
��1����E��- ��1����B�䣨0��-2����
��1����B�䣨0��-2�����õ�
 ��
�����

��ö��κ�������ʽy=-
 x2-
x2- x-2��
x-2����3���ܣ�������ֱ��EF���ҵ�P�㣻
����B��C��EF��P�㣬������BP��
����B��P=BP����ʱ��P��C��B����һ��ֱ���ϣ���BP+PC=B��P+PC�ĺ���С��
����BCΪ���������������PBC�ܳ���С��
��ֱ��B��C�Ľ���ʽΪ��y=kx+b�����У�
 ��
�����
 ��
����ֱ��B��C�Ľ���ʽΪ��y=-
 x-2��
x-2���֡�PΪֱ��B��C��ֱ��EF�Ľ��㣬
��
 ��
�����
 ��
�����P��������-
 ��-
��- ����
����������������Ҫ������һ�κ��������κ�������ʽ��ȷ������Գ�ͼ�ε����ʡ�����ͼ���֪ʶ���Ѷ�ƫ��

��ϰ��ϵ�д�
�����Ŀ
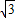 ��1����C��-3
��1����C��-3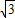 ��0����O��0��0�������˾������Ź�E��-
��0����O��0��0�������˾������Ź�E��-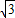 ��1����F��-
��1����F��-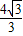 ��0����ֱ��EF�����·����ۣ�B��C�Ķ�Ӧ��ֱ�ΪB�䡢C�䣮
��0����ֱ��EF�����·����ۣ�B��C�Ķ�Ӧ��ֱ�ΪB�䡢C�䣮