��Ŀ����
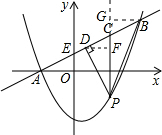
 ��2013•��������ģ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx+n��������y=ax2+bx-3����A��-2��0����B��4��3�����㣬��P��ֱ��AB�·����������ϵ�һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�C����PD��AB�ڵ�D��
��2013•��������ģ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx+n��������y=ax2+bx-3����A��-2��0����B��4��3�����㣬��P��ֱ��AB�·����������ϵ�һ���㣨�����A��B�غϣ�������P��x��Ĵ��߽�ֱ��AB�ڵ�C����PD��AB�ڵ�D����1����ֱ���������ߵĽ���ʽ��
��2�����P�ĺ�����Ϊm��
���ú�m�Ĵ���ʽ��ʾ�߶�PD�ij���������߶�PD�������ֵ��
������PB���߶�PC�ѡ�PDB�ֳ����������Σ��Ƿ�����ʺϵ�m��ֵ��ʹ�����������ε������Ϊ9��10�������ڣ�ֱ��д��m��ֵ���������ڣ���˵�����ɣ�
��������1����A��B�������y=kx+n�����k��n��ֵ��ȷ����ֱ�߽���ʽ����A��B������������߽���ʽ���a��b��ֵ������ȷ���������߽���ʽ��
��2������ֱ��AB��x�ύ�ڵ�E����CP��y��ƽ�У��õ���ACP=��AEO�����AE��OA�ij����ó�sin��AEO��ֵ����Ϊsin��ACP��ֵ����P�ĺ�����Ϊm���ֱ����ֱ���������߽���ʽ�õ�����������֮��ΪPC�ij�����PD=PCsin��ACP��ʾ��PD�����ö��κ������������PD�����ֵ���ɣ�
�ڴ��ڣ���D��DF��CP����B��BG��PQ����PC�ӳ������Q����ʾ��DF��BG��������ʾ��������DCP�����������BCP������������֮��Ϊ9��10�г�����m�ķ��̣�������̵Ľ�õ�m��ֵ���ɣ�
��2������ֱ��AB��x�ύ�ڵ�E����CP��y��ƽ�У��õ���ACP=��AEO�����AE��OA�ij����ó�sin��AEO��ֵ����Ϊsin��ACP��ֵ����P�ĺ�����Ϊm���ֱ����ֱ���������߽���ʽ�õ�����������֮��ΪPC�ij�����PD=PCsin��ACP��ʾ��PD�����ö��κ������������PD�����ֵ���ɣ�
�ڴ��ڣ���D��DF��CP����B��BG��PQ����PC�ӳ������Q����ʾ��DF��BG��������ʾ��������DCP�����������BCP������������֮��Ϊ9��10�г�����m�ķ��̣�������̵Ľ�õ�m��ֵ���ɣ�
��� �⣺��1����A��-2��0����B��4��3������ֱ��y=kx+n�У��ã�
�⣺��1����A��-2��0����B��4��3������ֱ��y=kx+n�У��ã�
��
��ã�
��
��ֱ�߽���ʽΪy=
x+1��
��A��-2��0����B��4��3�����������߽���ʽy=ax2+bx-3�ã�
��
��ã�
��
�������߽���ʽΪy=
x2-
x-3��
��2���١�PC��y�ᣬ
���ACP=��AEO��
����ֱ��y=
x+1����y=0���õ�x=-2����AO=2����x=0���õ�y=1����OE=1��
���ݹ��ɶ����õ�AE=
��
��sin��ACP=sin��AEO=
=
��
��x=m����ֱ�߽���ʽ�ã�y=
m+1�����������߽���ʽ�ã�y=
m2-
m-3��
��CP=��
m+1��-��
m2-
m-3��=-
m2+m+4��
��DP=CP•sin��ACP=��-
m2+m+4����
=-
��m-1��2+
��
��-
��0��
�൱m=1ʱ��DP�����ֵΪ
��
�ڴ��ڣ�
��D��DF��CP����B��BG��PQ����PC�ӳ������Q��
��sin��ACP=
��
��cos��ACP=
��
��Rt��PDF�У�DF=DP•sin��DPC=DP•cos��ACP=
����-
m2+m+4����
=-
��m2+2m-8����
�֡�BG=4-m��
��
=
=
=
=
��
��
=
=
ʱ����ã�m=
��
��
=
=
ʱ����ã�m=
��
 �⣺��1����A��-2��0����B��4��3������ֱ��y=kx+n�У��ã�
�⣺��1����A��-2��0����B��4��3������ֱ��y=kx+n�У��ã�
|
��ã�
|
��ֱ�߽���ʽΪy=
| 1 |
| 2 |
��A��-2��0����B��4��3�����������߽���ʽy=ax2+bx-3�ã�
|
��ã�
|
�������߽���ʽΪy=
| 1 |
| 2 |
| 1 |
| 2 |
��2���١�PC��y�ᣬ
���ACP=��AEO��
����ֱ��y=
| 1 |
| 2 |
���ݹ��ɶ����õ�AE=
| 5 |
��sin��ACP=sin��AEO=
| OA |
| AE |
2
| ||
| 5 |
��x=m����ֱ�߽���ʽ�ã�y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��CP=��
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��DP=CP•sin��ACP=��-
| 1 |
| 2 |
2
| ||
| 5 |
| ||
| 5 |
9
| ||
| 5 |
��-
| ||
| 5 |
�൱m=1ʱ��DP�����ֵΪ
9
| ||
| 5 |
�ڴ��ڣ�
��D��DF��CP����B��BG��PQ����PC�ӳ������Q��
��sin��ACP=
2
| ||
| 5 |
��cos��ACP=
| ||
| 5 |
��Rt��PDF�У�DF=DP•sin��DPC=DP•cos��ACP=
| ||
| 5 |
| 1 |
| 2 |
2
| ||
| 5 |
| 1 |
| 5 |
�֡�BG=4-m��
��
| S��DCP |
| S��BCP |
| ||
|
| DF |
| BG |
-
| ||
| 4-m |
| m+2 |
| 5 |
��
| S��DCP |
| S��BCP |
| m+2 |
| 5 |
| 9 |
| 10 |
| 5 |
| 2 |
��
| S��DCP |
| S��BCP |
| m+2 |
| 5 |
| 10 |
| 9 |
| 32 |
| 9 |
���������⿼���˶��κ����ۺ��⣬�漰��֪ʶ�У�����ϵ������������ʽ��������ͼ�����ʣ����κ�����ͼ�������ʣ�������Ǻ������壬ͬ�����Ǻ�����Ļ�����ϵ���Լ������ε�������������մ���ϵ�����ǽⱾ���һ�ʵĹؼ���

��ϰ��ϵ�д�
 Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�
�����Ŀ
 ��2013•��������ģ����ͼ����ֱ֪������ABCD�У�AD��BC����BAD=90�㣬AD=2��AB=4��BC=5����PΪAB����һ���㣬����PC��PD������PCDΪֱ�������Σ������������ĵ�P�У�������
��2013•��������ģ����ͼ����ֱ֪������ABCD�У�AD��BC����BAD=90�㣬AD=2��AB=4��BC=5����PΪAB����һ���㣬����PC��PD������PCDΪֱ�������Σ������������ĵ�P�У������� ��2013•��������ģ����ͼ����б�߳�Ϊ1�ĵ���ֱ��������OAB�У����ڽ�������A1B1D1C1���ڵ���ֱ��������OA1B1�����ڽ�������A2B2D2C2���ڵ���ֱ��������OA2B2�����ڽ�������A3B3D3C3��������������ȥ�����n��������AnBnDnCn�ı߳���
��2013•��������ģ����ͼ����б�߳�Ϊ1�ĵ���ֱ��������OAB�У����ڽ�������A1B1D1C1���ڵ���ֱ��������OA1B1�����ڽ�������A2B2D2C2���ڵ���ֱ��������OA2B2�����ڽ�������A3B3D3C3��������������ȥ�����n��������AnBnDnCn�ı߳���
 ��2013•��������ģ����ͼ����֪�㣨1��2���ں���y=
��2013•��������ģ����ͼ����֪�㣨1��2���ں���y=