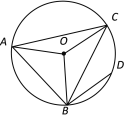
[题目]如图.△ABC是⊙O的内接三角形.点D是弧BC的中点.已知∠AOB=98°.∠COB=120°．则∠ABD的度数是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，△ABC是⊙O的内接三角形，点D是弧BC的中点，已知∠AOB=98°，∠COB=120°．则∠ABD的度数是___．

【答案】101°

【解析】试题分析：根据周角为360°，可求出∠AOC的度数，由圆周角定理可求出∠ABC的度数，关键是求∠CBD的度数；由于D是弧BC的中点，根据圆周角定理知∠DBC=∠BAC，而∠BAC的度数可由同弧所对的圆心角∠BOC的度数求得，由此得解．

解：∵∠AOB=98°，∠COB=120°，

∴∠AOC=360°-∠AOB-∠COB=142°；

∴∠ABC=71°；

∵D是的中点，

∴∠CBD=∠BAC；

又∵∠BAC=∠COB=60°，

∴∠CBD=30°；

∴∠ABD=∠ABC+∠CBD=101°．

练习册系列答案

相关题目

【题目】如图，一只甲虫在5×5的方格(每个小格边长为1)上沿着网格线运动．它从A处出发去看望B，C，D处的其他甲虫．规定：向上、向右走为正，向下、向左走为负．如果从A到B记为：A→B(＋1，＋4)，从B到A记为：B→A(－1，－4)，其中第一个数表示左右方向，第二个数表示上下方向．

(1)图中B→C(____，____)，C→____(＋1，____)；

(2)若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程．

【题目】Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．

（1）若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2= °；

（2）若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间有何关系？说明理由．

（3）若点P在Rt△ABC斜边BA的延长线上运动（CE＜CD），则∠α、∠1、∠2之间有何关系？猜想并说明理由．

【题目】若三角形的两条边的长度是4cm和9cm，则第三条边的长度可能是（　　）

A. 4 cmB. 5 cmC. 9 cmD. 13 cm

【题目】填写下列空格，完成证明．
已知：如图，AD是△ABC的角平分线，点E在BC上，点F在CA的延长线上，EF∥AD，EF交AB于点G．
求证：∠3=∠F
证明：因为AD是△ABC的角平分线（已知）
所以∠1=∠2 （）
因为EF∥AD（已知）
所以∠3=∠（）
∠F=∠（）
所以∠3=∠F（）．

【题目】王老师对本班40名学生的血型作了统计，列出如下的统计表，则本班A型血的人数是( )

组别	A型	B型	AB型	O型
频率	0.4	0.35	0.1	0.15

A. 16人 B. 14人 C. 4人 D. 6人

【题目】把角度21.3°化成度、分、秒的形式：．

【题目】如图，禁止捕鱼期间，某海上稽查队在某海域巡逻，上午某一时刻在A处接到指挥部通知，在他们东北方向距离12海里的B处有一艘捕鱼船，正在沿南偏东75°方向以每小时10海里的速度航行，稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发，在C处成功拦截捕鱼船，求巡逻船从出发到成功拦截捕鱼船所用的时间.

试题分类