题目内容
已知方程组 的解x,y的值互为相反数,求a的值及原方程组的解.
的解x,y的值互为相反数,求a的值及原方程组的解.
解:根据三元一次方程组的概念,可由上题得到三元一次方程组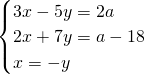 ,
,
把③代入①、②可得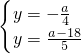 ,
,
解得a=8,
则y=-x=-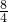 =-2,
=-2,
即原方程组的解为 .
.
分析:根据三元一次方程组解的概念,列出三元一次方程组解出x,y的值(含a),再进行计算.
点评:本题的实质是考查三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.
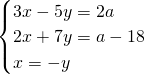 ,
,把③代入①、②可得
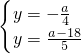 ,
,解得a=8,
则y=-x=-
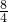 =-2,
=-2,即原方程组的解为
 .
.分析:根据三元一次方程组解的概念,列出三元一次方程组解出x,y的值(含a),再进行计算.
点评:本题的实质是考查三元一次方程组的解法.需要对三元一次方程组的定义有一个深刻的理解.方程组有三个未知数,每个方程的未知项的次数都是1,并且一共有三个方程,像这样的方程组,叫三元一次方程组.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.

练习册系列答案
相关题目
 的解x,y都是正数,求m的取值范围.(6分)
的解x,y都是正数,求m的取值范围.(6分) 的解为
的解为 ,那么一次函数y= 与一次函数y= 的交点为(2,4).
,那么一次函数y= 与一次函数y= 的交点为(2,4). 的解为
的解为 ,则函数y=2x+3与
,则函数y=2x+3与 的交点坐标为 .
的交点坐标为 . 的解为
的解为 则2a-3b的值为
则2a-3b的值为  的解x、y 的和为12,求n 的值.
的解x、y 的和为12,求n 的值.