题目内容
已知a、b是方程t2-t-1=0的两个实根，解方程组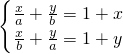
解：∵a，b是方程t2-t-1=0的两个实数根，
∴a+b=1，ab=-1，
原方程组化为：
把两方程相加得：（a+b）（x+y）=-2-（x+y），
解得x+y=-1
∴
分析：根据一元二次方程根与系数的关系，可知a+b=1，ab=-1，然后将方程组化简便可解出方程组．
点评：由根与系数的关系可得到a+b和ab的值，把a+b和ab的值代入转化后的方程组可将方程组化简，由方程组的特点可求出方程组的解．
∴a+b=1，ab=-1，
原方程组化为：
把两方程相加得：（a+b）（x+y）=-2-（x+y），
解得x+y=-1
∴
分析：根据一元二次方程根与系数的关系，可知a+b=1，ab=-1，然后将方程组化简便可解出方程组．
点评：由根与系数的关系可得到a+b和ab的值，把a+b和ab的值代入转化后的方程组可将方程组化简，由方程组的特点可求出方程组的解．
练习册系列答案
导学全程练创优训练系列答案
相关题目
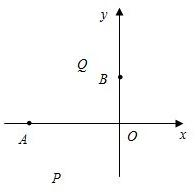象经过点A（t1，0），B（0，t2）．
x2+bx+c的图象经过点A（t1，0），B（0，t2）．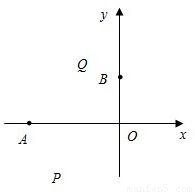
x2+bx+c的图象经过点A（t1，0），B（0，t2）．
x2+bx+c的图象经过点A（t1，0），B（0，t2）．