题目内容
如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.
【小题1】求证:DE是⊙O的切线
【小题2】若DE=3,⊙O的半径为5,求BF的长
【小题1】证明:如图(1)连接OD. 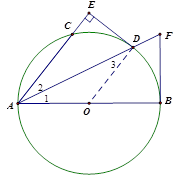
∵AD平分∠BAC, ∴∠1=∠2.
又∵OA="OD" ,∴∠1=∠3.
∴∠2="∠3."
∴OD∥AE.
∵DE⊥AE,
∴DE⊥OD.
而D在⊙O上,
∴DE是⊙O的切线.
【小题2】BF=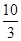
解析 (2)过D作DG⊥AB 于G.
∵DE⊥AE ,∠1=∠2.
∴DG="DE=3" ,半径OD=5.
在Rt△ODG中,根据勾股定理: OG=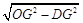 =
=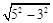 =4,
=4,
∴AG=AO+OG=5+4=9.
∵FB是⊙O的切线, AB是直径,
∴FB⊥AB.而DG⊥AB,
∴DG∥FB. △ADG∽△AFB,
∴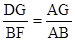 ∴
∴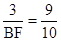 . ∴BF=
. ∴BF=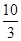 .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |
 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为