题目内容
如图1,四边形ABCD是一张矩形纸片,∠BAC=α(0°<α<45°),现将其折叠,使A,C两点重合.(1)作出折痕EF;
(2)设AC=x,EF=y,求出y与x的函数关系式;
(3)如图2,当45°<α<90°时,(2)题中求得的函数关系式是否成立?若成立,请说明理由;若不成立,请求出当45°<α<90°时,y与x的函数关系式.

【答案】分析:(1)作AC的中垂线EF,交AB、CD与E、F,EF即为折痕;
(2)连接CE、AF,则四边形AFCE为菱形,即OE=OF,OA=OC,AC⊥EF.在RT△AOE中,AO= x,OE=
x,OE= y,且OE=tanα•OA,由此以得到所求函数关系;
y,且OE=tanα•OA,由此以得到所求函数关系;
(3)当45°<α<90°时,
∵∠CAB=α,
∴∠DAO=90°-α.在Rt△AOF中,OF=tan(90°-α)•OA,有成可以求出函数关系.
解答: 解:(1)如图,作AC的中垂线与CD,AB分别交于F,E.EF即为折痕;
解:(1)如图,作AC的中垂线与CD,AB分别交于F,E.EF即为折痕;
(2)设AC与EF交于O点,则点O是矩形的对称中心,
∴AO= x,OE=
x,OE= y.
y.
在Rt△AOE中,OE=tanα•OA,
即y=xtanα.
(3)当45°<α<90°时,
∵∠CAB=α,∴∠FAO=90°-α.
所以(2)题中求得的函数关系式不成立.
在Rt△AOF中,OF=tan(90°-α)•OA,
即y=xcotα.
点评:此题主要考查了三角函数中正切和余切的运用,题目虽复杂,但解题相对简单.
(2)连接CE、AF,则四边形AFCE为菱形,即OE=OF,OA=OC,AC⊥EF.在RT△AOE中,AO=
 x,OE=
x,OE= y,且OE=tanα•OA,由此以得到所求函数关系;
y,且OE=tanα•OA,由此以得到所求函数关系;(3)当45°<α<90°时,
∵∠CAB=α,
∴∠DAO=90°-α.在Rt△AOF中,OF=tan(90°-α)•OA,有成可以求出函数关系.
解答:
 解:(1)如图,作AC的中垂线与CD,AB分别交于F,E.EF即为折痕;
解:(1)如图,作AC的中垂线与CD,AB分别交于F,E.EF即为折痕;(2)设AC与EF交于O点,则点O是矩形的对称中心,
∴AO=
 x,OE=
x,OE= y.
y.在Rt△AOE中,OE=tanα•OA,
即y=xtanα.
(3)当45°<α<90°时,
∵∠CAB=α,∴∠FAO=90°-α.
所以(2)题中求得的函数关系式不成立.
在Rt△AOF中,OF=tan(90°-α)•OA,
即y=xcotα.
点评:此题主要考查了三角函数中正切和余切的运用,题目虽复杂,但解题相对简单.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
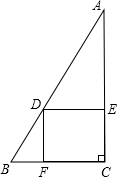 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y. 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( ) 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD. 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.