题目内容
如图，△ABC，AB=12，AC=15，D为AB上一点，且AD=| 2 |
| 3 |
A、
| ||
| B、10 | ||
C、
| ||
| D、以上答案都不对 |
分析：△ADE与△ABC相似，则存在两种情况，即△AED∽△ACB，也可能是△AED∽△ABC，应分类讨论，求解．
解答：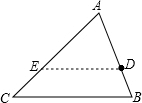
解：如图
（1）当∠AED=∠C时，即DE∥BC
则AE=
AC=10
（2）当∠AED=∠B时，△AED∽△ABC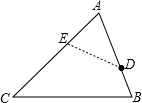
∴
=
，即
=
AE=
综合（1），（2），故选C．
解：如图（1）当∠AED=∠C时，即DE∥BC
则AE=
| 2 |
| 3 |
（2）当∠AED=∠B时，△AED∽△ABC
∴
| AE |
| AB |
| AD |
| AC |
| AE |
| 12 |
| 8 |
| 15 |
AE=
| 32 |
| 5 |
综合（1），（2），故选C．
点评：会利用相似三角形求解一些简单的计算问题．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC中AB=AC，AD⊥BC，垂足为点D，∠BAC=48°，CE、CF三等分∠ACB，分别交AD于点E、F，连接BE并延长交AC于点G，连接FG，则∠AGF=
15、如图，△ABC中AB=AC，EB=BD=DC=CF，∠A=40°，则∠EDF的度数是
如图，△ABC，AB=AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，有下列四个结论：
如图，△ABC中AB=AC，AD是角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F．下列结论中，不正确的是（ ）