题目内容
![]() 是等边三角形,点
是等边三角形,点![]() 是射线
是射线![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() 重合),
重合),![]() 是以
是以![]() 为边的等边三角形,过点
为边的等边三角形,过点![]() 作
作![]() 的平行线,分别交射线
的平行线,分别交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
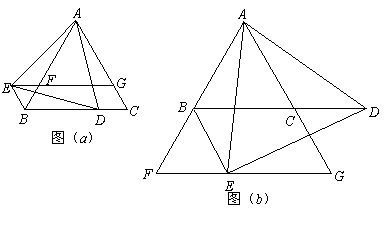
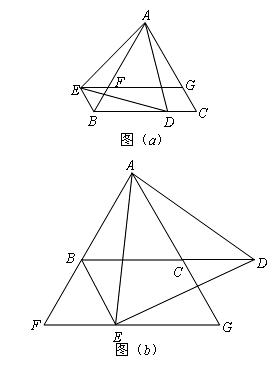
(1)如图(a)所示,当点![]() 在线段
在线段![]() 上时.
上时.
①求证:![]() ;
;
②探究四边形![]() 是怎样特殊的四边形?并说明理由;
是怎样特殊的四边形?并说明理由;
(2)如图(b)所示,当点![]() 在
在![]() 的延长线上时,直接写出(1)中的两个结论是否成立?
的延长线上时,直接写出(1)中的两个结论是否成立?
(3)在(2)的情况下,当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形?并说明理由.
是菱形?并说明理由.
 |
(1)①证明:∵![]() 和
和![]() 都是等边三角形,
都是等边三角形,
 ∴
∴![]() .??????? 1分
.??????? 1分
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
②法一:由①得![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
法二:证出![]() ,
,
得![]() .
.
由①得![]() .
.
得![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
(2)①②都成立.
 (3)当
(3)当![]() (
(![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() )时,四边形
)时,四边形![]() 是菱形.
是菱形.
理由:法一:由①得![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() .
.
由②得四边形![]() 是平行四边形,
是平行四边形,
∴四边形![]() 是菱形.
是菱形.
法二:由①得![]() ,
,
∴![]() .
.
又∵四边形![]() 是菱形,
是菱形,
∴![]()
∴![]() .
.
法三:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]()
∴![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
又∵![]() ,四边形
,四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
 33、如图所示,△ABC是等边三角形,点是AC的中点,过D点作DM⊥BE,垂足是MD;延长BC到E,使CE=CD,求证:BM=EM.
33、如图所示,△ABC是等边三角形,点是AC的中点,过D点作DM⊥BE,垂足是MD;延长BC到E,使CE=CD,求证:BM=EM. 是等边三角形,点
是等边三角形,点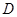 是射线
是射线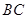 上的一个动点(点
上的一个动点(点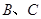 重合),
重合), 是以
是以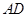 为边的等边三角形,过点
为边的等边三角形,过点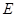 作
作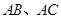 于点
于点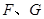 ,连接
,连接 .
.
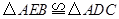 ;
; 是怎样特殊的四边形?并说明理由;
是怎样特殊的四边形?并说明理由;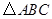 是等边三角形,点
是等边三角形,点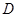 是射线
是射线 上的一个动点(点
上的一个动点(点 重合),
重合),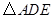 是以
是以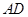 为边的等边三角形,过点
为边的等边三角形,过点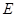 作
作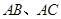 于点
于点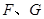 ,连接
,连接 .
.
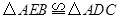 ;
;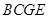 是怎样特殊的四边形?并说明理由;
是怎样特殊的四边形?并说明理由; 是等边三角形,点
是等边三角形,点 是
是 上任意一点,
上任意一点, 分别与两边垂直,等边三角形的高为
分别与两边垂直,等边三角形的高为 ,则
,则 的值为
的值为
