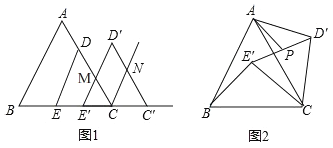题目内容
【题目】已知![]() ,H为射线OA上一定点,
,H为射线OA上一定点,![]() ,P为射线OB上一点,M为线段OH上一动点,连接PM,满足
,P为射线OB上一点,M为线段OH上一动点,连接PM,满足![]() 为钝角,以点P为中心,将线段PM顺时针旋转
为钝角,以点P为中心,将线段PM顺时针旋转![]() ,得到线段PN,连接ON.
,得到线段PN,连接ON.
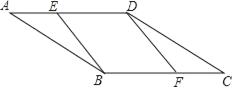
(1)依题意补全图1;
(2)求证:![]() ;
;
(3)点M关于点H的对称点为Q,连接QP.写出一个OP的值,使得对于任意的点M总有ON=QP,并证明.
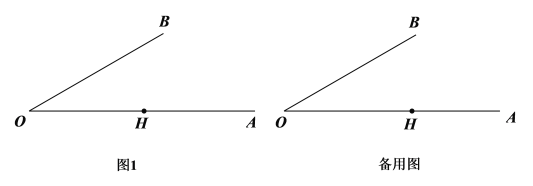
【答案】(1)如图所示见解析;(2)见解析;(3)OP=2.证明见解析.
【解析】
(1)根据题意画出图形即可.
(2)由旋转可得∠MPN=150°,故∠OPN=150°-∠OPM;由∠AOB=30°和三角形内角和180°可得∠OMP=180°-30°-∠OPM=150°-∠OPM,得证.
(3)根据题意画出图形,以ON=QP为已知条件反推OP的长度.由(2)的结论∠OMP=∠OPN联想到其补角相等,又因为旋转有PM=PN,已具备一边一角相等,过点N作NC⊥OB于点C,过点P作PD⊥OA于点D,即可构造出△PDM≌△NCP,进而得PD=NC,DM=CP.此时加上ON=QP,则易证得△OCN≌△QDP,所以OC=QD.再设DM=CP=x,所以OC=OP+PC=2+x,MH=MD+DH=x+1,由于点M、Q关于点H对称,得出DQ=DH+HQ=1+x+1=2+x,得出OC=DQ,再利用SAS得出△OCN≌△QDP即可
解:(1)如图1所示为所求.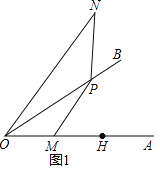
(2)设∠OPM=α,
∵线段PM绕点P顺时针旋转150°得到线段PN
∴∠MPN=150°,PM=PN
∴∠OPN=∠MPN-∠OPM=150°-α
∵∠AOB=30°
∴∠OMP=180°-∠AOB-∠OPM=180°-30°-α=150°-α
∴∠OMP=∠OPN
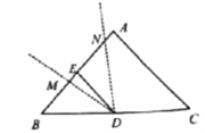
(3)OP=2时,总有ON=QP,证明如下:
过点N作NC⊥OB于点C,过点P作PD⊥OA于点D,如图2
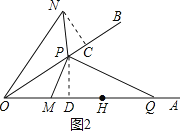
∴∠NCP=∠PDM=∠PDQ=90°
∵∠AOB=30°,OP=2
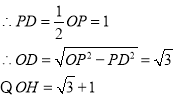
∴DH=OH-OD=1
∵∠OMP=∠OPN
∴180°-∠OMP=180°-∠OPN
即∠PMD=∠NPC
在△PDM与△NCP中
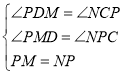
∴△PDM≌△NCP(AAS)
∴PD=NC,DM=CP
设DM=CP=x,则OC=OP+PC=2+x,MH=MD+DH=x+1
∵点M关于点H的对称点为Q
∴HQ=MH=x+1
∴DQ=DH+HQ=1+x+1=2+x
∴OC=DQ
在△OCN与△QDP中
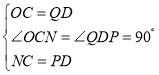
∴△OCN≌△QDP(SAS)
∴ON=QP

 阅读快车系列答案
阅读快车系列答案【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() ,角的两边分别交直线
,角的两边分别交直线![]() 于
于![]() 两点,设
两点,设![]() 点间的距离为
点间的距离为![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
小涛根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
(1)列表:下表的已知数据是根据![]() 两点间的距离
两点间的距离![]() 进行取点、画图、测量,分别得到了 与 的几组对应值:
进行取点、画图、测量,分别得到了 与 的几组对应值:
| 0 | 0.30 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| 3.00 | 3.50 | 3.68 | 3.81 | 3.90 | 3.93 | 4.10 |
| 2.88 | 2.81 | 2.69 | 2.67 | 2.80 | 3.15 | 3.85 | 5.24 | 6.01 | 6.71 | 7.27 | 7.44 | 8.87 |
请你通过计算,补全表格
(2)描点、连线:在平面直角坐标系![]() 中,描出表中各组数值所对应的点
中,描出表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 关于
关于![]() 的图象:
的图象:

(3)探究性质:随着自变量![]() 的不断增大,函数
的不断增大,函数![]() 的变化趋势:
的变化趋势:
(4)解决问题:当![]() 时,
时,![]() 的长度大约是____
的长度大约是____![]() (保留两位小数).
(保留两位小数).