Question

（2002•武汉）已知：如图，E是相交两圆⊙M和⊙N的一个交点，且ME⊥NE，AB为外公切线，切点分别为A，B连接AE，BE，则∠AEB的度数为（ ）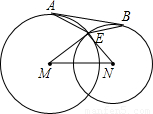

A．145°
B．140°
C．135°
D．130°

Answer 1

【答案】分析：连接AM，BN，根据弦切角定理得∠BAE+∠ABE=（∠AME+∠BNE）；结合MA⊥AB，NB⊥AB可得∠AMN+∠BNM=180°，所以进一步推导得∠AME+∠BNE=180°-90°=90°，则∠BAE+∠ABE=×90°=45°，利用三角形内角和可得∠AEB的值．
解答：解：连接AM，BN，
∵∠BAE=∠AME，∠ABM=∠BNE，
∴∠BAE+∠ABE=（∠AME+∠BNE），
∵MA⊥AB，NB⊥AB，
∴MA∥NB，
∴∠AMN+∠BNM=180°．
∵∠MEN=90°，
∴∠EMN+∠ENM=90°，
∴∠AME+∠BNE=180°-90°=90°，
∴∠BAE+∠ABE=×90°=45°，
∴∠AEB=180°-45°=135°．
故选C．
点评：此题较复杂，解答此题的关键是，利用切线的性质构造出直角三角形，再根据等腰三角形及直角三角形的性质解答．