题目内容
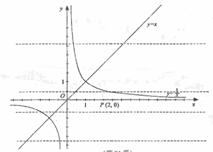
已知平行于x轴的直线![]() 与函数
与函数![]() 和函数
和函数![]() 的图象分别交于点A和点B,又有定点P(2,0) .
的图象分别交于点A和点B,又有定点P(2,0) .
(1)若![]() ,且tan∠POB=
,且tan∠POB=![]() ,求线段AB的长;
,求线段AB的长;
(2)在过A,B两点且顶点在直线![]() 上的抛物线中,已知线段AB=
上的抛物线中,已知线段AB=![]() ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
(3)已知经过A,B,P三点的抛物线,平移后能得到![]() 的图象,求点P到直线AB的距离
的图象,求点P到直线AB的距离
. 
(1)设第一象限内的点B(m,n),则tan∠POB![]() ,得m=9n,又点B在函数
,得m=9n,又点B在函数![]() 的图象上,得
的图象上,得![]() ,所以m=3(-3舍去),点B为
,所以m=3(-3舍去),点B为![]() ,
,
而AB∥x轴,所以点A(![]() ,
,![]() ),所以
),所以![]() ;
;
(2)由条件可知所求抛物线开口向下,设点A(a , a),B(![]() ,a),则AB=
,a),则AB=![]() - a =
- a = ![]() ,
,
所以![]() ,解得
,解得![]() .
.
当a = -3时,点A(3,3),B(![]() ,3),因为顶点在y = x上,所以顶点为(-
,3),因为顶点在y = x上,所以顶点为(-![]() ,-
,-![]() ),所以可设二次函数为
),所以可设二次函数为![]() ,点A代入,解得k= -
,点A代入,解得k= -![]() ,所以所求函数解析式为
,所以所求函数解析式为![]() .
.
同理,当a = ![]() 时,所求函数解析式为
时,所求函数解析式为![]() ;
;
(3)设A(a , a),B(![]() ,a),由条件可知抛物线的对称轴为
,a),由条件可知抛物线的对称轴为![]() .
.
设所求二次函数解析式为:![]() .
.
点A(a , a)代入,解得![]() ,
,![]() ,所以点P到直线AB的距离为3或
,所以点P到直线AB的距离为3或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
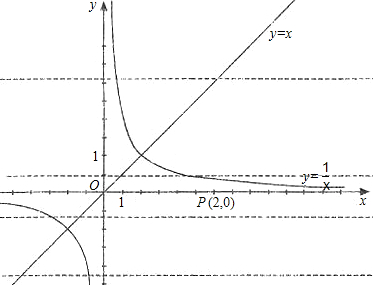
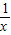 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.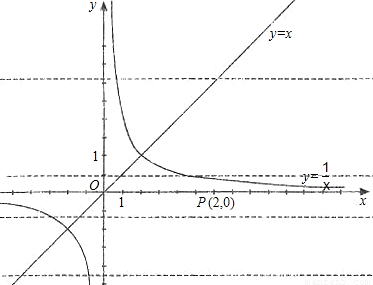
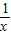 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.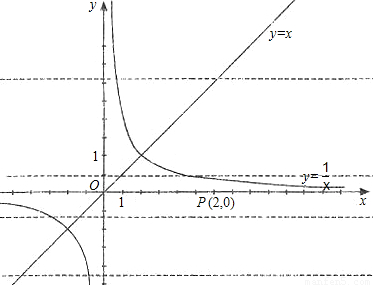
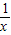 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.
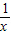 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0). ,求线段AB的长;
,求线段AB的长; ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式; x2的图象,求点P到直线AB的距离.
x2的图象,求点P到直线AB的距离.