题目内容
如图①,直线![]()
![]() 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且![]()
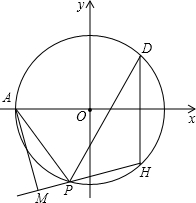
![]() ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
(1)写出A、B、C三点的坐标,并求抛物线的解析式;(5分)
(2) 当△BDE是等腰三角形时,直接写出此时点E的坐标;(3分)
(3)连结PC、PB,△PBC是否有最大面积?若有,求出△PBC的最大面积和此时P点的坐标;若没有,请说明理由。(3分)
 |
 |
(3)相切。证明略
(3)P点坐标为![]()
![]()
【解析】解:(1)A(-1,0),B(3,0),C(0,-3) ————3分
设抛物线解析式为
![]()
![]() ,把C(0,-3)代入得
,把C(0,-3)代入得![]()
![]() ,解得a=1.
,解得a=1.
∴抛物线的解析式为
![]() . ————2分
. ————2分

=
![]()
∴当![]()
![]() 时,△PBC的面积的面积最大,最大面积为
时,△PBC的面积的面积最大,最大面积为![]()
![]() , ————1分
, ————1分
此时P点坐标为![]()
![]() .
. ![]() ————1分
————1分

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
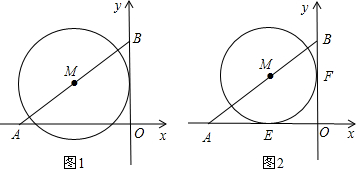


 图象上点B处.
图象上点B处. 与x轴、y轴分别交于点E、F,点P为反比例函数在第一象限图象上一动点,PG⊥x轴于G,交线段EF于M,PH⊥y轴于H,交线段EF于N.当点P运动时,∠MON的度数是否改变?如果改变,试说明理由;如果不变,请求其度数.
与x轴、y轴分别交于点E、F,点P为反比例函数在第一象限图象上一动点,PG⊥x轴于G,交线段EF于M,PH⊥y轴于H,交线段EF于N.当点P运动时,∠MON的度数是否改变?如果改变,试说明理由;如果不变,请求其度数.