题目内容
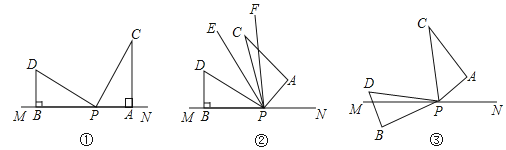
【题目】如图，有一副直角三角板如图①放置（其中
，
），
、
与直线
重合，且三角板
，三角板
均可以绕点
逆时针旋转.
（l）直接写出
等于多少度．
（2）如图②，若三角板保持不动，三角板
绕点逆时针旋转，转速为
/秒，转动一周三角板就停止转动，在旋转的过程中，当旋转时间为多少时，有
成立.
（3）如图③，在图①基础上，若三角板的边从
.处开始绕点逆时针旋转，转速为
/秒，同时三角板的边从
处开始绕点逆时针旋转，转速为
/秒，（当
转到与重合时，两三角板都停止转动），在旋转过程中，当
，求旋转的时间是多少？
【答案】（1）
；（2）
和
（3）
.
【解析】
（1）根据
计算即可；
（2）分边PC在直线MN上方和下方两种情况进行讨论即可；
（3）设运动时间为t秒，
，
，根据题意用t表示出∠CPD和∠BPN的度数即可得出答案．
（1）∵一副直角三角板
，
∴
,
∴
=
（2）第一种情况：当边PC在直线MN上方时，
如图所示，此时
成立，
∵，
，
∴
.
∵
，
∴
.
∴
.
∵三角板
的转速为
/秒，
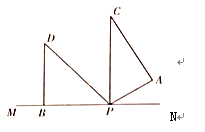
∴旋转时间为.
第二种情况：边PC在直线MN下方时，
如图所示，此时成立，
∵，，
∴
.
∵，
∴.
∴
.
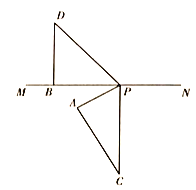
∴三角板旋转的角度是
.
∵三角板的转速为/秒，
∴旋转时间为.
综上所述，当旋转时间为和时，有成立.
（3）设旋转的时间是
秒，
由题知，，，
∴
，
∴
.
∵
，
∴
.
解得
，
∴当时，旋转的时间为.
练习册系列答案
阅读快车系列答案
相关题目
