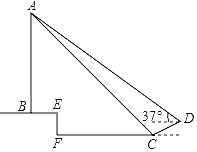
题目内容
【题目】在![]() 中,
中,![]() ,以
,以![]() 为斜边作等腰直角三角形
为斜边作等腰直角三角形![]() ,且点
,且点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,连接
的两侧,连接![]() .
.
(1)如图1,若![]() ,则
,则![]() 的度数为______.
的度数为______.
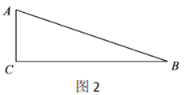
(2)已知![]() ,
,![]() .
.
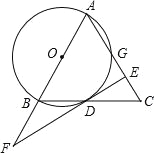
①依题意将图2补全;
②求![]() 的长;
的长;
小聪通过观察、实验、提出猜想,与同学们进行交流,通过讨论,形成了求![]() 长的几种想法:
长的几种想法:
想法1:延长![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,连接
,连接![]() .要求
.要求![]() 的长,需证明
的长,需证明![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
想法2:过点![]() 作
作![]() 于点
于点![]() ,
,![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,要求
,要求![]() 的长,需证明
的长,需证明![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
……
请参考上面的想法,帮助小聪求出![]() 的长(一种方法即可).
的长(一种方法即可).
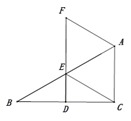
(3)用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系(直接写出即可).
之间的数量关系(直接写出即可).
【答案】(1)105度;(2)①将图2补全见解析;②![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出∠CAB=60°,再利用等腰直角三角形求出∠BAD=45°,进而求出∠CAD;
(2)①根据题意及基本作图即可补全图形;延长![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,连接
,连接![]() .要求
.要求![]() 的长,需证明
的长,需证明![]() ,
,![]() 为等腰直角三角形再利用等腰直角三角形的性质即可得出解;
为等腰直角三角形再利用等腰直角三角形的性质即可得出解;
(3)同(2)的方法即可得出结论.
(1)∵![]() ,
,![]()
∴∠CAB=90°-∠ABC=60°
∵△![]() 是等腰直角三角形,
是等腰直角三角形,
∴∠BAD=45°
∴![]() =∠CAB+∠BAD=105°
=∠CAB+∠BAD=105°
故答案为:105°.
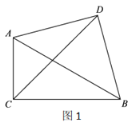
(2)①补全图形,如图2所示.
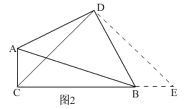
②延长![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,
,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD=180°.
∵∠DBE+∠CBD=180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∵AC=1,BC=3,
∴CE=4.
∵CE2=CD2+DE2,
∴42=CD2+CD2
∴CD=![]() .
.
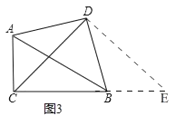
(3)AC+BC=![]() CD,
CD,
理由:如图3,延长![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,
,
∵∠ACB=∠ADB=90°,
∴∠CAD+∠CBD=180°.
∵∠DBE+∠CBD=180°,
∴∠CAD=∠DBE.
∵DA=DB,AC=BE,
∴△ACD≌△BED.
∴DC=DE,∠ADC=∠BDE.
∴∠CDE=90°.
∴△CDE为等腰直角三角形.
∴CE2=CD2+DE2,
∴CE=![]() CD,
CD,
∵CE=BC+BE=BC+AC.
即:AC+BC=![]() CD.
CD.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案