Question

【题目】已知：如图，在△ABC中，∠BAC=120°，以BC为边向形外作等边三角形△BCD，把△ABD绕着点D按顺时针方向旋转60°后得到△ECD，若AB=5，AC=3，求AD的长．

Answer 1

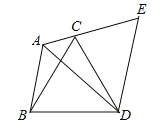
【答案】8

【解析】

只要证明△ADE是等边三角形，即可推出∠EAD=60°，AD=AE，推出∠BAD=∠BAC-∠CAD=60°，推出AD=AE=AC+CE=AC+AB=3+5=8．

∵△ECD 由△ABD 绕点 D 顺时针旋转 60°而得：

∴AD=DE，∠BDA=∠CDE，

∴∠BDC=∠ADE=60°，∠ABD=∠ECD，

∵∠BAC=120°，∠BDC=60°，

∴∠BAC+∠BDC=180°，

∴∠ABD+∠ACD=180°，

∴∠ACD+∠ECD=180°，

∴A、C、E 共线，

∴△ADE 是等边三角形，

∴∠EAD=60°，AD=AE，

∴AD=AE=AC+CE=AC+AB=3+5=8．