题目内容
已知二次函数y=ax2+bx+c的图象经过(-1,0),(3,0),(1,2)三点,求这个二次函数的解析式和该抛物线上纵坐标为 的点的横坐标.
的点的横坐标.
解:设二次函数解析式为y=a(x+1)(x-3),
把点(1,2)的坐标代入y=a(x+1)(x-3)中得:2=a(1+1)×(1-3),
解得:a=- ,
,
∴抛物线解析式为:y=- (x+1)(x-3),即y=-
(x+1)(x-3),即y=- x2+x+
x2+x+ ,
,
当y= 时,则有-
时,则有- x2+x+
x2+x+ =
= ,
,
解得:x1=0或x2=2,
则抛物线上纵坐标为 的点的横坐标为0或2.
的点的横坐标为0或2.
分析:由抛物线与x轴的两交点坐标,设出二次函数的两根式,将(1,2)代入求出a的值,确定出二次函数解析式,令y= 得到关于x的方程,求出方程的解即可得到所求点的横坐标.
得到关于x的方程,求出方程的解即可得到所求点的横坐标.
点评:此题考查了利用待定系数法求二次函数的解析式,用待定系数法求函数的解析式时要灵活地根据已知条件选择配方法和公式法,这种方法是数学中一种重要的数学方法.
把点(1,2)的坐标代入y=a(x+1)(x-3)中得:2=a(1+1)×(1-3),
解得:a=-
 ,
,∴抛物线解析式为:y=-
 (x+1)(x-3),即y=-
(x+1)(x-3),即y=- x2+x+
x2+x+ ,
,当y=
 时,则有-
时,则有- x2+x+
x2+x+ =
= ,
,解得:x1=0或x2=2,
则抛物线上纵坐标为
 的点的横坐标为0或2.
的点的横坐标为0或2.分析:由抛物线与x轴的两交点坐标,设出二次函数的两根式,将(1,2)代入求出a的值,确定出二次函数解析式,令y=
 得到关于x的方程,求出方程的解即可得到所求点的横坐标.
得到关于x的方程,求出方程的解即可得到所求点的横坐标.点评:此题考查了利用待定系数法求二次函数的解析式,用待定系数法求函数的解析式时要灵活地根据已知条件选择配方法和公式法,这种方法是数学中一种重要的数学方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
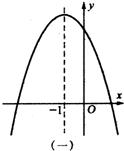 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
