Question

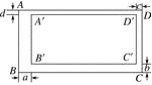
【题目】如图一，矩形中，，，是上一点，将沿折叠,使点落在上一点处，连结、．

求的长度；

设点、、分别在线段、、上，当且四边形为矩形时，请说明矩形的长宽比为，并求的长．（如图二）

Answer 1

【答案】（1）BE=1.5；（2）证明见解析；PE=.

【解析】

（1）先根据矩形性质以及折叠变换，运用勾股定理求得AF、BF的长，再设BE＝，在Rt△BEF中运用勾股定理列出方程，求得的值．

（2）先判断PH垂直平分BC，求得矩形中BH的长，再根据平行线分线段成比例定理，求得PH的长，进而得出矩形BGPH的长宽比为2：1，最后根据勾股定理求得PE的长．

解：如图一，在矩形中，，，，

由折叠可得：，，

∴直角三角形中，，

∴，

设，则，

在中，，

解得，

即；

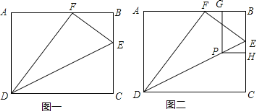
如图二，当，且四边形为矩形时，点在的垂直平分线上，

即垂直平分，

∴，①

又∵，

∴，

∵，

∴，即

解得，②

∴由①②得：矩形的长宽比为，

在中，．