题目内容
如图,在正方形网格中,点O、A的坐标分别为(0,0)、(5,0),将△OAB绕点 O按逆时针方向旋转90°得到△OA′B′.
O按逆时针方向旋转90°得到△OA′B′.
(1)在正方形网格中作出△OA′B′;
(2)写出点B′的坐标,并求出AA′的长;
(3)求出△A′AB的面积.
解:(1)所作图形如下所示:
(2)根据图形可得:B′(-2,6),
Rt△OAA′中,∵OA=OA′=5,
∴AA′= .
.
(3)△A′AB面积=SOA'B+SOAB-S△OA′A= ×4×5+
×4×5+ ×4×2-
×4×2- ×4×4=20.
×4×4=20.
分析:(1)根据旋转角度、旋转中心、旋转方向可确定各点的对应点,顺次连接即可得出.
(2)根据图形即可写出B′点的坐标,运用勾股定理可得出AA′的长.
(3)将三角形的面积分为两个三角形计算即可直接算出.
点评:本题考查旋转作图及三角形的面积求法,属于综合题,但是难度不大,关键还是根据旋转的定义准确作出图形.

(2)根据图形可得:B′(-2,6),
Rt△OAA′中,∵OA=OA′=5,
∴AA′=
 .
.(3)△A′AB面积=SOA'B+SOAB-S△OA′A=
 ×4×5+
×4×5+ ×4×2-
×4×2- ×4×4=20.
×4×4=20.分析:(1)根据旋转角度、旋转中心、旋转方向可确定各点的对应点,顺次连接即可得出.
(2)根据图形即可写出B′点的坐标,运用勾股定理可得出AA′的长.
(3)将三角形的面积分为两个三角形计算即可直接算出.
点评:本题考查旋转作图及三角形的面积求法,属于综合题,但是难度不大,关键还是根据旋转的定义准确作出图形.

练习册系列答案
相关题目
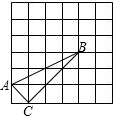 如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )
如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
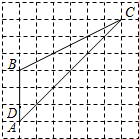 如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=
如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE= 6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
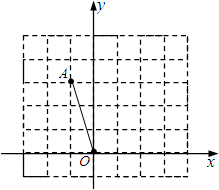 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).