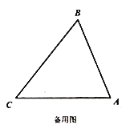
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΈ“Ο«Α―’ΐ![]() ±Ώ–Έ(
±Ώ–Έ(![]() )ΒΡΗς±Ώ»ΐΒ»Ζ÷Θ§Ζ÷±π“‘Ψ”÷–ΒΡΡ«ΧθœΏΕΈΈΣ“Μ±ΏœρΆβΉς’ΐ
)ΒΡΗς±Ώ»ΐΒ»Ζ÷Θ§Ζ÷±π“‘Ψ”÷–ΒΡΡ«ΧθœΏΕΈΈΣ“Μ±ΏœρΆβΉς’ΐ![]() ±Ώ–ΈΘ§≤Δ»ΞΒτΨ”÷–ΒΡΡ«ΧθœΏΕΈΘ§ΒΟΒΫ“ΜΗω–¬ΒΡΆΦ–ΈΫ–Ήω’ΐ
±Ώ–ΈΘ§≤Δ»ΞΒτΨ”÷–ΒΡΡ«ΧθœΏΕΈΘ§ΒΟΒΫ“ΜΗω–¬ΒΡΆΦ–ΈΫ–Ήω’ΐ![]() ±Ώ–ΈΒΡΓΑά©’ΙΆΦ–ΈΓ±Θ§≤ΔΫΪΥϋΒΡ±Ώ ΐΦ«ΈΣ
±Ώ–ΈΒΡΓΑά©’ΙΆΦ–ΈΓ±Θ§≤ΔΫΪΥϋΒΡ±Ώ ΐΦ«ΈΣ![]() Θ§»γΆΦ
Θ§»γΆΦ![]() Θ§ΫΪ’ΐ»ΐΫ«–ΈΫχ––…œ ω≤ΌΉςΚσΒΟΒΫΤδΓΑά©’ΙΆΦ–ΈΓ±Θ§«“
Θ§ΫΪ’ΐ»ΐΫ«–ΈΫχ––…œ ω≤ΌΉςΚσΒΟΒΫΤδΓΑά©’ΙΆΦ–ΈΓ±Θ§«“![]() .ΆΦ
.ΆΦ![]() ΓΔΆΦ
ΓΔΆΦ![]() Ζ÷±π «’ΐΈε±Ώ–ΈΓΔ’ΐΝυ±Ώ–ΈΒΡΓΑά©’ΙΆΦ–ΈΓ±ΓΘ
Ζ÷±π «’ΐΈε±Ώ–ΈΓΔ’ΐΝυ±Ώ–ΈΒΡΓΑά©’ΙΆΦ–ΈΓ±ΓΘ
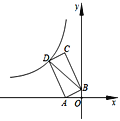
(1)»γΆΦ![]() Θ§‘Ύ
Θ§‘Ύ![]() ΒΡ’ΐΖΫ–ΈΆχΗώ÷–”ΟΫœ¥÷ΒΡ–ιœΏΜ≠”–“ΜΗω’ΐΖΫ–ΈΘ§«κ‘ΎΆΦ
ΒΡ’ΐΖΫ–ΈΆχΗώ÷–”ΟΫœ¥÷ΒΡ–ιœΏΜ≠”–“ΜΗω’ΐΖΫ–ΈΘ§«κ‘ΎΆΦ![]() ÷–”Ο ΒœΏΜ≠≥ω¥Υ’ΐΖΫ–ΈΒΡΓΑά©’ΙΆΦ–ΈΓ±ΘΜ
÷–”Ο ΒœΏΜ≠≥ω¥Υ’ΐΖΫ–ΈΒΡΓΑά©’ΙΆΦ–ΈΓ±ΘΜ
(2)“―÷Σ![]() Θ§‘ρΆΦ
Θ§‘ρΆΦ![]() ÷–
÷–![]() =_____Θ§ΗυΨί“‘…œΙφ¬…Θ§’ΐ
=_____Θ§ΗυΨί“‘…œΙφ¬…Θ§’ΐ![]() ±Ώ–ΈΒΡΓΑά©’ΙΆΦ–ΈΓ±ΒΡ
±Ώ–ΈΒΡΓΑά©’ΙΆΦ–ΈΓ±ΒΡ![]() =______ΘΜ(”ΟΚ§
=______ΘΜ(”ΟΚ§![]() ΒΡ ΫΉ”±μ Ψ)
ΒΡ ΫΉ”±μ Ψ)
(3)“―÷Σ![]() Θ§«“
Θ§«“![]() Θ§‘ρ
Θ§‘ρ![]() =_____.
=_____.
ΓΨ¥πΑΗΓΩ(1)ΦϊΫβΈωΘΜ(2)42Θ§![]() ΘΜ(3)99.
ΘΜ(3)99.
ΓΨΫβΈωΓΩ
1Θ©ΗυΨίΧβΡΩ“Σ«σΜ≠≥ωΆΦ–ΈΦ¥Ω…ΘΜ
Θ®2Θ©ΗυΨί![]() Θ§Ω…ΒΟ
Θ§Ω…ΒΟ![]() =42Θ§‘ΌΗυΨίΗΟΙφ¬…’“≥ω
=42Θ§‘ΌΗυΨίΗΟΙφ¬…’“≥ω![]() Φ¥Ω…ΘΜ
Φ¥Ω…ΘΜ
Θ®3Θ©ΗυΨίΥυΗχΒΡ ΫΉ”ΒΡΙφ¬…Θ§»ΜΚσΝ–≥ωΙΊ”ΎnΒΡΖΫ≥ΧΘ§ΉνΚσ‘ΌΫχ––Ϋβ¥πΦ¥Ω….
ΫβΘΚ(1)»γΆΦΥυ ΨΘΚ

Θ®2Θ©ΫβΘΚΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
“άΗΟΙφ¬…Ω…ΒΟΘΚ![]() .
.
Ι ¥πΑΗΈΣ42ΘΜn(n+1).
Θ®3Θ©ΫβΘΚΓΏ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§...Θ§
Θ§...Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΫβΒΟΘΚn=99.
Ι ¥πΑΗΈΣ99.

 ΉΏΫχΈΡ―‘ΈΡœΒΝ–¥πΑΗ
ΉΏΫχΈΡ―‘ΈΡœΒΝ–¥πΑΗ