题目内容
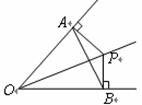
在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证: Rt△AB E≌Rt△CBF;
E≌Rt△CBF;
(2)若∠CAE=30º,求∠ACF度数.
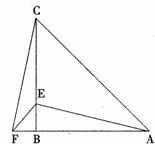
解:(1)∵∠ABC=90°,∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF, AB=BC, ∴Rt△ABE≌Rt△CBF(HL)
(2) ∵AB=BC, ∠ABC=90°, ∴ ∠CAB=∠AC B=45°.
B=45°.
∵∠BAE=∠CAB-∠CA E=45°-30°=15°.
E=45°-30°=15°.
由(1)知 Rt△ABE≌Rt△CBF, ∴∠BCF=∠BAE= 15°,
15°,
∴∠ACF= ∠BCF+∠ACB=45°+15°=60°.
∠BCF+∠ACB=45°+15°=60°.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目




 ,
,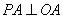 ,
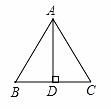
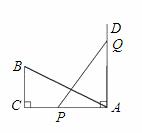
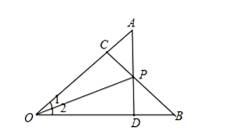
,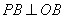 ,垂足分别为A,B.下列结论中不一定成立的是( )
,垂足分别为A,B.下列结论中不一定成立的是( )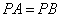 B.
B.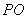 平分
平分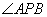 C.
C.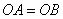 D.
D.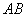 垂直平分
垂直平分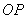
 数,我们叫它“回文数”.回文数实际上是由左右排列对称的自然数构成的,有趣的是,当你遇到一个普通的数(两位以上),经过一定的计算,可以变成“回文数”,办法很简单:只要将这个数加上它的逆序数就可以了,若一次不成功,反复进行下去,一定能得到一个回文
数,我们叫它“回文数”.回文数实际上是由左右排列对称的自然数构成的,有趣的是,当你遇到一个普通的数(两位以上),经过一定的计算,可以变成“回文数”,办法很简单:只要将这个数加上它的逆序数就可以了,若一次不成功,反复进行下去,一定能得到一个回文 数,比如:
数,比如: ②362
②362