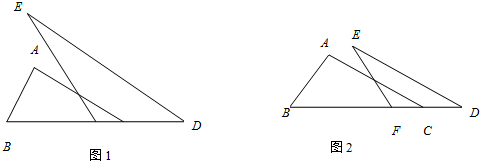Question

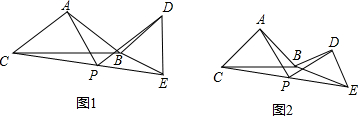
如图1，在△ABC和△EDC中，AC＝CE＝CB＝CD，∠ACB＝∠ECD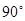＝，AB与CE交于F，ED与AB、BC分别交于M、H．

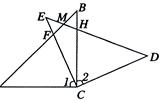
图1

(1)求证:CF＝CH；

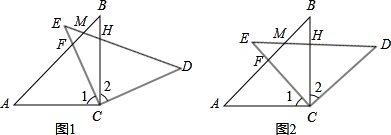
(2)如图2，△ABC不动，将△EDC绕点C旋转到∠BCE=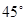时，试判断四边形ACDM是什么四边形？并证明你的结论．

                  

图2

 

Answer 1

【答案】

（1）通过证明△ACB≌△ECD，从而得出CF＝CH

（2）ACDM是菱形

【解析】

试题分析：(1) 证明:在△ACB和△ECD中，

∵∠ACB=∠ECD=，∴∠1+∠ECB=∠2+∠ECB, ∴∠1=∠2．…………………1分

又∵AC=CE=CB=CD,  ∴∠A=∠D=．∴△ACB≌△ECD ．……………………2分

∴CF="CH" ． …………………………………………………………………………3分

(2) 四边形ACDM是菱形． ……………………………………………………………4分

证明: ∵∠ACB=∠ECD=, ∠BCE=，∴∠1=, ∠2=．  …………5分

又∵∠E=∠B=,∴∠1=∠E, ∠2=∠B．  …………………………………6分

∴AC∥MD,  CD∥AM ． ∴ACDM是平行四边形． …………………………7分

又∵AC=CD,  ∴ACDM是菱形．  ……………………………………………8分

考点：三角形的全等、菱形的判定、旋转的性质

点评：此题是简单题，主要要求学生熟悉并熟练运用三角形全等的判定与菱形的判定。