Question

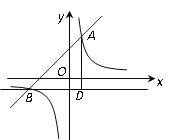
【题目】如图，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为（2，4）；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3．

（1）求该抛物线所对应的函数关系式；

（2）将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）．

①当t=时，判断点P是否在直线ME上，并说明理由；

②设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）①不在；②最大值为．

【解析】

试题分析：（1）已知顶点坐标，又抛物线经过原点，用待定系数可求出抛物线解析式；

（2）①根据抛物线的对称性求出E点坐标，再求出直线ME的解析式，把t知代入验证点P是否在直线ME上；

②最后一问设出P，N坐标，根据几何关系求出PN，然后分两种情况讨论：（1）PN=0；（2）PN≠0；把求多边形面积S转化为求函数最值问题．

试题解析：（1）因所求抛物线的顶点M的坐标为（2，4），故可设其关系式为，又∵抛物线经过O（0，0），∴得，解得a=﹣1，∴所求函数关系式为，即．

（2）①点P不在直线ME上．根据抛物线的对称性可知E点的坐标为（4，0），又M的坐标为（2，4），设直线ME的关系式为y=kx+b．于是得：，解得：，所以直线ME的关系式为y=﹣2x+8．

由已知条件易得，当t=时，OA=AP=，∴P（，）．

∵P点的坐标不满足直线ME的关系式y=﹣2x+8，∴当t=时，点P不在直线ME上．

②S存在最大值．理由如下：

∵点A在x轴的非负半轴上，且N在抛物线上，∴OA=AP=t，∴点P，N的坐标分别为（t，t）、（t，），∴AN=（0≤t≤3），∴AN﹣AP=（）﹣t==t（3﹣t）≥0，∴PN=．（ⅰ）当PN=0，即t=0或t=3时，以点P，N，C，D为顶点的多边形是三角形，此三角形的高为AD，∴S=DCAD=×3×2=3．

（ⅱ）当PN≠0时，以点P，N，C，D为顶点的多边形是四边形．

∵PN∥CD，AD⊥CD，∴S=（CD+PN）AD= ==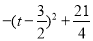，其中（0＜t＜3），由a=﹣1，0＜＜3，此时S最大=．

综上所述，当t=时，以点P，N，C，D为顶点的多边形面积有最大值，这个最大值为．

说明：（ⅱ）中的关系式，当t=0和t=3时也适合．