题目内容
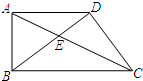 已知:如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线AC、BD相交于点E,BD⊥CD,AB=12,cot∠ADB=
已知:如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线AC、BD相交于点E,BD⊥CD,AB=12,cot∠ADB= .
.
求:(1)∠DBC的余弦值;
(2)DE的长.
解:(1)∵Rt△ABD中,cot∠ADB= ,
,
∴ =
=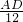 ,
,
则AD=16,
∴BD= =
=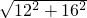 =20,
=20,
∵AD∥BC,
∴∠DBC=∠ADB,
∴cos∠DBC=cos∠ADB=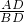 =
=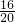 =
= ;
;
(2)在Rt△BCD中,cos∠DBC= ,
,
即 =
=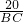 ,
,
解得:BC=25,
∵AD∥BC,
∴ =
= =
= ,
,
∴ =
=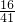 ,
,
∴DE=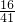 ×BD=
×BD=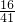 ×20=
×20=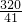 .
.
分析:(1)根据cot∠ADB= ,可求出AD的长度,在Rt△ABD中利用勾股定理求出BD,继而可得出∠DBC的余弦值;
,可求出AD的长度,在Rt△ABD中利用勾股定理求出BD,继而可得出∠DBC的余弦值;
(2)在Rt△BDC中,由(1)的答案可求出BC的长度,再由平行线分线段成比例的知识可求出DE的长.
点评:本题考查了梯形、勾股定理及平行线分线段成比例的知识,解答本题的关键是熟练掌握解直角三角形的方法,能正确表示角的三角函数.
 ,
,∴
 =
=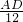 ,
,则AD=16,
∴BD=
 =
=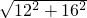 =20,
=20,∵AD∥BC,
∴∠DBC=∠ADB,
∴cos∠DBC=cos∠ADB=
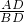 =
=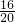 =
= ;
;(2)在Rt△BCD中,cos∠DBC=
 ,
,即
 =
=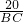 ,
,解得:BC=25,
∵AD∥BC,
∴
 =
= =
= ,
,∴
 =
=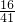 ,
,∴DE=
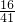 ×BD=
×BD=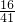 ×20=
×20=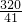 .
.分析:(1)根据cot∠ADB=
 ,可求出AD的长度,在Rt△ABD中利用勾股定理求出BD,继而可得出∠DBC的余弦值;
,可求出AD的长度,在Rt△ABD中利用勾股定理求出BD,继而可得出∠DBC的余弦值;(2)在Rt△BDC中,由(1)的答案可求出BC的长度,再由平行线分线段成比例的知识可求出DE的长.
点评:本题考查了梯形、勾股定理及平行线分线段成比例的知识,解答本题的关键是熟练掌握解直角三角形的方法,能正确表示角的三角函数.

练习册系列答案
相关题目
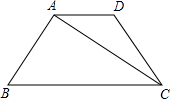 已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,求AC的长及梯形面积S.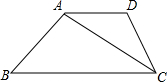 已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,
已知:如图,在梯形ABCD中,AD∥BC,∠B=45°,∠BAC=105°,AD=CD=4,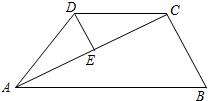 已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=
已知:如图,在梯形ABCD中,AB∥CD,AC⊥BC,AC平分∠DAB,点E为AC的中点.求证:DE=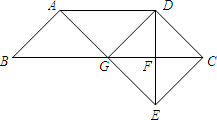 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G. 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.