题目内容
如图,在直角梯形中,
∥
,
,点
为坐标原点,点
在
轴的正半轴上,对角线
,
相交于点
,
,
.
(1)线段的长为 ,点
的坐标为 ;
(2)求△的面积;
(3)求过,
,
三点的抛物线的解析式;
(4)若点在(3)的抛物线的对称轴上,点
为该抛物线上的点,且以
,
,
,
四点为顶点的四边形为平行四边形,求点
的坐标.
(1)4 ;
(2)
(3)
(4)点F的坐标为,
解析:解:(1)4 ;
. …………………(2分)
(2)在直角梯形OABC中,OA=AB=4,
∵ ∥
∴ △OAM∽△BCM ………(3分)
又 ∵ OA=2BC
∴ AM=2CM ,CM=AC ………………(4分)
所以 ………(5分)
(注:另有其它解法同样可得结果,正确得本小题满分.)
(3)设抛物线的解析式为
由抛物线的图象经过点,
,
.所以
……………………………(6分)
解这个方程组,得,
,
………………(7分)
所以抛物线的解析式为 ………………(8分)
(4)∵ 抛物线的对称轴是CD,
① 当点E在轴的下方时,CE和OA互相平分则可知四边形OEAC为平行四边形,此时点F和点C重合,点F的坐标即为点
; …(9分)
② 当点E在轴的下方,点F在对称轴
的右侧,存在平行四边形
,
∥
,且
,此时点F的横坐标为6,将
代入
,可得
.所以
. ………………………………………(11分)
同理,点F在对称轴的左侧,存在平行四边形
,
∥
,且
,此时点F的横坐标为
,将
代入
,可得
.所以
.(12分)
综上所述,点F的坐标为,
. ………(12分)

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 20、如图,在直角梯形中,底AD=6 cm,BC=11 cm,腰CD=12 cm,则这个直角梯形的周长为
20、如图,在直角梯形中,底AD=6 cm,BC=11 cm,腰CD=12 cm,则这个直角梯形的周长为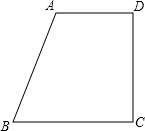 如图,在直角梯形中,AD=6cm,BC=11cm,CD=12cm,则AB的长为
如图,在直角梯形中,AD=6cm,BC=11cm,CD=12cm,则AB的长为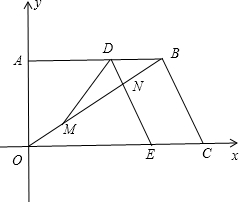 DE由CB出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM.若没运动时间为t(s)(0<t<8).
DE由CB出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM.若没运动时间为t(s)(0<t<8). 如图,在直角梯形中,上底AC=6cm,下底BD=11cm,CD⊥BD且腰CD=12cm,则这个直角梯形的周长为
如图,在直角梯形中,上底AC=6cm,下底BD=11cm,CD⊥BD且腰CD=12cm,则这个直角梯形的周长为 中,
中, ,
, ,
, ,
, .
. 边上一点,过点
边上一点,过点 作EF⊥DC于点F.求证
作EF⊥DC于点F.求证 .
.