题目内容
（2003•河北）如图，E是边长为1的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值是（ ）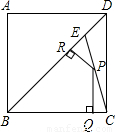
A．
B．
C．
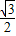
D．
【答案】分析：连接BP，利用面积法求解，PQ+PR的值等于C点到BE的距离，即正方形对角线的一半．
解答：
解：连接BP，过C作CM⊥BD，
∵S△BCE=S△BPE+S△BPC
=BC×PQ×
+BE×PR×
=BC×（PQ+PR）×
=BE×CM×
，BC=BE，
∴PQ+PR=CM，
∵BE=BC=1且正方形对角线BD=
=
，
又BC=CD，CM⊥BD，
∴M为BD中点，又△BDC为直角三角形，
∴CM=
BD=
，
即PQ+PR值是
．
故选A．
点评：本题的解题关键是作出正确的辅助线，利用全等三角形的判定和性质的应用，来化简题目．
解答：
解：连接BP，过C作CM⊥BD，∵S△BCE=S△BPE+S△BPC
=BC×PQ×
+BE×PR×=BC×（PQ+PR）×
=BE×CM×，BC=BE，∴PQ+PR=CM，
∵BE=BC=1且正方形对角线BD=
=，又BC=CD，CM⊥BD，
∴M为BD中点，又△BDC为直角三角形，
∴CM=
BD=，即PQ+PR值是
．故选A．
点评：本题的解题关键是作出正确的辅助线，利用全等三角形的判定和性质的应用，来化简题目．
练习册系列答案
阅读快车系列答案
相关题目
（2003•河北）如图：MN为⊙O的切线，A为切点，过点A作AP⊥MN交⊙O的弦BC于点P，若PA=2cm，PB=5cm，PC=3cm．则⊙O的直径为
