题目内容
下列命题中为真命题的是
- A.有一个角是40°的两个等腰三角形相似
- B.三点一定可以确定一个圆
- C.圆心角的度数相等,则圆心角所对的弧相等
- D.三角形的内心到三角形三边距离相等
D
分析:A、不知道40°的角是底角还是顶角,无法判断相似;
B、三点共线不能确定圆;
C、要有在同圆或等圆中的条件;
D、根据三角形内心的性质进行判断.
解答:当一个等腰三角形的顶角等于40°而另一个等腰三角形的底角是40°,则这两个三角形不相似,所以A错;
只有不共线的三点才确定一个圆,所以B错;
只有在同圆或等圆中,圆心角的度数相等,则圆心角所对的弧相等,所以C错;
内心就是三角形角平分线的交点,则它到三角形三边的距离相等,所以D对.
故选D.
点评:有两个角对应相等的三角形相似.记住三点不共线确定一个圆;只有在同圆或等圆中,圆心角的度数相等,则圆心角所对的弧相等.
分析:A、不知道40°的角是底角还是顶角,无法判断相似;
B、三点共线不能确定圆;
C、要有在同圆或等圆中的条件;
D、根据三角形内心的性质进行判断.
解答:当一个等腰三角形的顶角等于40°而另一个等腰三角形的底角是40°,则这两个三角形不相似,所以A错;
只有不共线的三点才确定一个圆,所以B错;
只有在同圆或等圆中,圆心角的度数相等,则圆心角所对的弧相等,所以C错;
内心就是三角形角平分线的交点,则它到三角形三边的距离相等,所以D对.
故选D.
点评:有两个角对应相等的三角形相似.记住三点不共线确定一个圆;只有在同圆或等圆中,圆心角的度数相等,则圆心角所对的弧相等.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
下列命题中为真命题的是( )
| A、同位角相等 | ||||
B、-
| ||||
| C、若a是无理数,a2则为有理数 | ||||
| D、等腰三角形两腰上的高相等 |
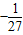 的立方根是±
的立方根是±
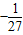 的立方根是±
的立方根是±