Question

【题目】如图，已知，是直线上的点，．

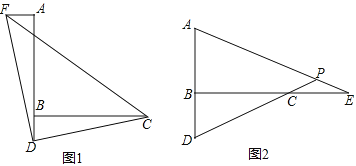
（1）如图1，过点作，并截取，连接、、，判断的形状并证明；

（2）如图2，是直线上一点，且，直线、相交于点，的度数是一个固定的值吗？若是，请求出它的度数；若不是，请说明理由．

Answer 1

【答案】（1）是等腰三角形；（2）．

【解析】

试题分析：

（1）利用证明和全等，再利用全等三角形的性质得出，即可判断三角形的形状；

（2）作于，使，连结，，利用证明和全等，再利用全等三角形的性质得出，，即可得出．

试题解析：

解:（1）是等腰三角形，理由如下：

∵，，

∴，

在与中，

∵，，，

∴，

∴，

∵

∴，即

∴是等腰三角形；

（2）作于，使，连结，，如图，

∵，，

∴，

在与中，

∵，，，

∴，

∴，

∴是等腰三角形，

∵，

∴，

∵，

∴，

∴是等腰直角三角形，

∴，

∵，且，

∴四边形是平行四边形，

∴，

∴

又∵

∴．

点拨：（1）是“三垂直”模型的直接应用，在遇到这样模型时应首先尝试证

（2）在（1）的提示下，本题考查学生知识迁移的能力，尝试构造半弦图——“三垂直”来找到突破口，难度较大.