Question

【题目】如图，四边形ABCD是正方形，G是直线BC上的任意一点，DE⊥直线AG于点E．BF⊥直线AG于点F．

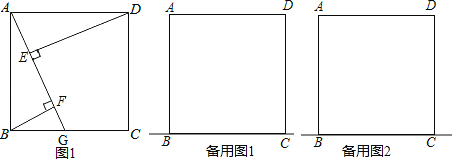
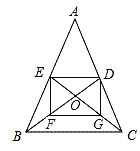
（1）如图1，若点G在线段BC上，判断AF，BF，EF之间的数量关系，并说明理由．

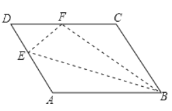
（2）若点G在CB延长线上，直接写出AF，BF，EF之间的数量关系．

（3）若点G在BC延长线上，直接写出AF，BF，EF之间的数量关系．

Answer 1

【答案】（1）AF＝EF+BF．理由见解析；（2）AF+EF＝BF；（3）AF+BF＝EF．

【解析】

（1）证明△BAF≌△ADE即可．
（2）与（1）一样，都是证明△BAF≌△ADE即可．

（3）与（1）一样，都是证明△BAF≌△ADE即可．

（1）如图1，AF=EF+BF．
理由如下：
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∵DE⊥AG，BF⊥AG，
∴∠AFB=∠DEA=90°，
又∵∠BAF+∠DAE=∠DAE+∠ADE=90°，
∴∠BAF=∠ADE，
在△BAF和△ADE中：

∴△BAF≌△ADE（AAS），
∴AE=BF，
∴AF=AE+EF=BF+EF．
（2）如图2，AF+EF=BF．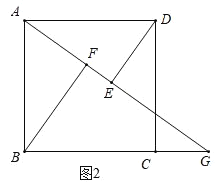

理由如下：
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∵DE⊥AG，BF⊥AG，
∴∠AFB=∠DEA=90°，
又∵∠BAF+∠DAE=∠DAE+∠ADE=90°，
∴∠BAF=∠ADE，
在△BAF和△ADE中：
，
∴△BAF≌△ADE（AAS），
∴AE=BF，
∴AF+EF=AE=BF．
（3）如图3，AF+BF=EF．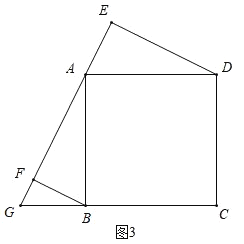

理由如下：
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∵DE⊥AG，BF⊥AG，
∴∠AFB=∠DEA=90°，
又∵∠BAF+∠DAE=∠DAE+∠ADE=90°，
∴∠BAF=∠ADE，
在△BAF和△ADE中：
，
∴△BAF≌△ADE（AAS），
∴AE=BF，
∴EF=AE+AF=BF+AF．