题目内容
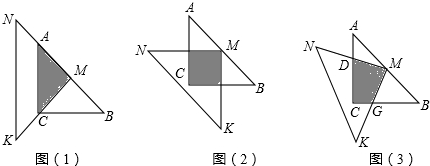
一位同学拿了两块45°三角尺△MNK,△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=4.
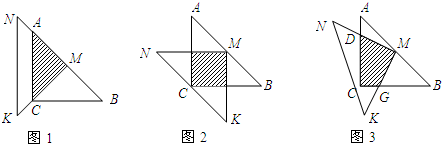
(1)如图1,两三角尺的重叠部分为△ACM,则重叠部分的面积为
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为
(3)如果将△MNK绕M旋转到不同于图1和图2的图形,如图3,请你猜想此时重叠部分的面积为
(4)在图3情况下,若AD=1,求出重叠部分图形的周长.

(1)如图1,两三角尺的重叠部分为△ACM,则重叠部分的面积为
4
4
,周长为4+4
| 2 |
4+4
.| 2 |
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为
4
4
,周长为8
8
.(3)如果将△MNK绕M旋转到不同于图1和图2的图形,如图3,请你猜想此时重叠部分的面积为
4
4
.(4)在图3情况下,若AD=1,求出重叠部分图形的周长.
分析:(1)根据AC=BC=4,∠ACB=90°,得出AB的值,再根据M是AB的中点,得出AM=MC,求出重叠部分的面积,再根据AM,MC,AC的值即可求出周长;
(2)易得重叠部分是正方形,边长为
AC,面积为
AC2,周长为2AC.
(3)过点M分别作AC、BC的垂线MH、ME,垂足为H、E.求得Rt△MHD≌Rt△MEG,则阴影部分的面积等于正方形CEMH的面积.
(4)先过点M作ME⊥BC于点E,MH⊥AC于点H,根据∠DMH=∠EMH,MH=ME,得出Rt△DHM≌Rt△EMG,从而得出HD=GE,CE=AD,最后根据AD和DF的值,算出DM=
,即可得出答案.
(2)易得重叠部分是正方形,边长为
| 1 |
| 2 |
| 1 |
| 4 |
(3)过点M分别作AC、BC的垂线MH、ME,垂足为H、E.求得Rt△MHD≌Rt△MEG,则阴影部分的面积等于正方形CEMH的面积.
(4)先过点M作ME⊥BC于点E,MH⊥AC于点H,根据∠DMH=∠EMH,MH=ME,得出Rt△DHM≌Rt△EMG,从而得出HD=GE,CE=AD,最后根据AD和DF的值,算出DM=
| 5 |
解答:解:(1)∵AC=BC=4,∠ACB=90°,
∴AB=
=
=4
,
∵M是AB的中点,
∴AM=2
,
∵∠ACM=45°,
∴AM=MC,
∴重叠部分的面积是
=4,
∴周长为:AM+MC+AC=2
+2
+4=4+4
;
故答案为:4,4+4
;
(2)∵叠部分是正方形,
∴边长为
×4=2,面积为
×4×4=4,
周长为2×4=8.
故答案为:4,8.
(3)过点M分别作AC、BC的垂线MH、ME,垂足为H、E,
∵M是△ABC斜边AB的中点,AC=BC=4,
∴MH=
BC,
ME=
AC,
∴MH=ME,
又∵∠NMK=∠HME=90°,
∴∠NMH+∠HMK=90°,∠EMG+∠HMK=90°,
∴∠HMD=∠EMG,
在△MHD和△MEG中,
∵
,
∴△MHD≌△MEG(ASA),
∴阴影部分的面积等于正方形CEMH的面积,
∵正方形CEMH的面积是ME•MH=
×4×
×4=4;
∴阴影部分的面积是4;
故答案为:4.
(4)如图所示:
过点M作ME⊥BC于点E,MH⊥AC于点H,
∴四边形MECH是矩形,
∴MH=CE,
∵∠A=45°,
∴∠AMH=45°,
∴AH=MH,
∴AH=CE,
在Rt△DHM和Rt△GEM中,
,
∴Rt△DHM≌Rt△GEM.
∴GE=DH,
∴AH-DH=CE-GE,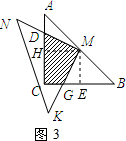
∴CG=AD,
∵AD=1,
∴DH=1.
∴DM=
=
∴四边形DMGC的周长为:
CE+CD+DM+ME
=AD+CD+2DM=4+2
.
∴AB=
| AC2+BC2 |
| 42+42 |
| 2 |
∵M是AB的中点,
∴AM=2
| 2 |
∵∠ACM=45°,
∴AM=MC,
∴重叠部分的面积是
2
| ||||
| 2 |
∴周长为:AM+MC+AC=2
| 2 |
| 2 |
| 2 |
故答案为:4,4+4
| 2 |
(2)∵叠部分是正方形,
∴边长为
| 1 |
| 2 |
| 1 |
| 4 |
周长为2×4=8.
故答案为:4,8.
(3)过点M分别作AC、BC的垂线MH、ME,垂足为H、E,
∵M是△ABC斜边AB的中点,AC=BC=4,
∴MH=
| 1 |
| 2 |
ME=
| 1 |
| 2 |
∴MH=ME,
又∵∠NMK=∠HME=90°,
∴∠NMH+∠HMK=90°,∠EMG+∠HMK=90°,
∴∠HMD=∠EMG,
在△MHD和△MEG中,
∵
|
∴△MHD≌△MEG(ASA),
∴阴影部分的面积等于正方形CEMH的面积,
∵正方形CEMH的面积是ME•MH=
| 1 |
| 2 |
| 1 |
| 2 |
∴阴影部分的面积是4;
故答案为:4.
(4)如图所示:
过点M作ME⊥BC于点E,MH⊥AC于点H,
∴四边形MECH是矩形,
∴MH=CE,
∵∠A=45°,
∴∠AMH=45°,
∴AH=MH,
∴AH=CE,
在Rt△DHM和Rt△GEM中,
|
∴Rt△DHM≌Rt△GEM.
∴GE=DH,
∴AH-DH=CE-GE,

∴CG=AD,
∵AD=1,
∴DH=1.
∴DM=
| 1+4 |
| 5 |
∴四边形DMGC的周长为:
CE+CD+DM+ME
=AD+CD+2DM=4+2
| 5 |
点评:此题考查了等腰直角三角形,利用等腰直角三角形的性质,等腰直角三角形的面积公式,正方形的面积公式,全等三角形的判定和性质求解.

练习册系列答案
相关题目
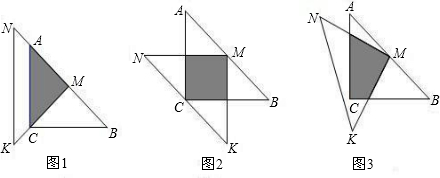
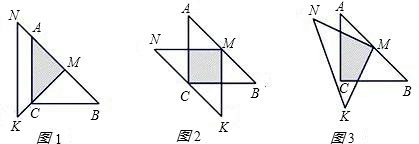
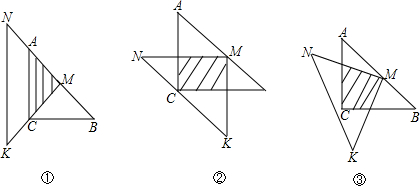
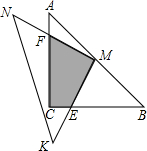 如图所示,一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动;将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
如图所示,一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动;将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.